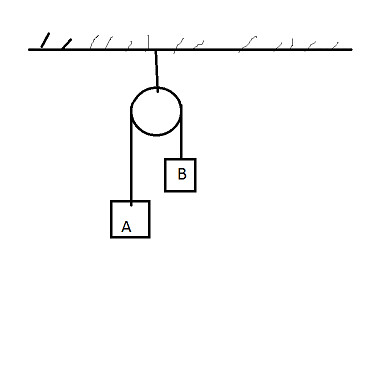
In the arrangement shown in the figure #M_a\ "and"\ M_b# are #2\ "Kg and"\ 1\ "Kg" #respectively .Find the acceleration of center of massof both the blocks Neglect friction everywhere . ?

Question

2723 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-02T09:05:13

See below.

Considering

#x_g = (m_ax_a+m_b x_b)/(m_a+m_b)# as the system center of mass

we have

#ddot x_g = (m_a ddot x_a+m_b ddot x_b)/(m_a+m_b)#

For each mass we have

#{(T-m_a g = m_a ddot x_a),(T-m_b g = m_b ddot x_b):}#

but due to the fact that the rope is inextensible

#ddot x_a = -ddot x_b = a# and substituting and resolving for #a# we have

#a = ((m_b-m_a)/(m_a+m_b)) g# now substituting into the formula for #ddot x_g# we have

#ddot x_g = -((m_a - m_b)/(m_a + m_b))^2g#