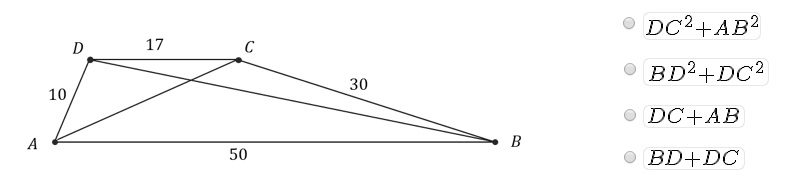
In the below figure, the measures of the sides of the Trapazoid ABCD are given. If the non-parallel sides of the Trapazoid are perpendicular then #AC^2 + BD^2 = # ?

enter image source here

1 Answer
CW
Sep 22, 2017

#DC^2+AB^2#

Explanation:

enter image source here
Extend #AD and BC# such that they meet at #E#, as shown in the figure.
Given that #AD# is perpendicular to #BC#,
#=> DeltaAEB# is right-angled at #E#.
By Pythagorean theorem,
#AC^2=AE^2+CE^2#
#BD^2=DE^2+BE^2#
Similarly,
#AB^2=AE^2+BE^2#
#CD^2=CE^2+DE^2#
#=> AC^2+BD^2=AE^2+CE^2+DE^2+BE^2#
#=> AC^2+BD^2=(AE^2+BE^2)+(CE^2+DE^2)#
#=> AC^2+BD^2=AB^2+CD^2#

Hence, # AC^2+BD^2=DC^2+AB^2#

Related questions
Impact of this question
3555 views around the world
You can reuse this answer
Creative Commons License