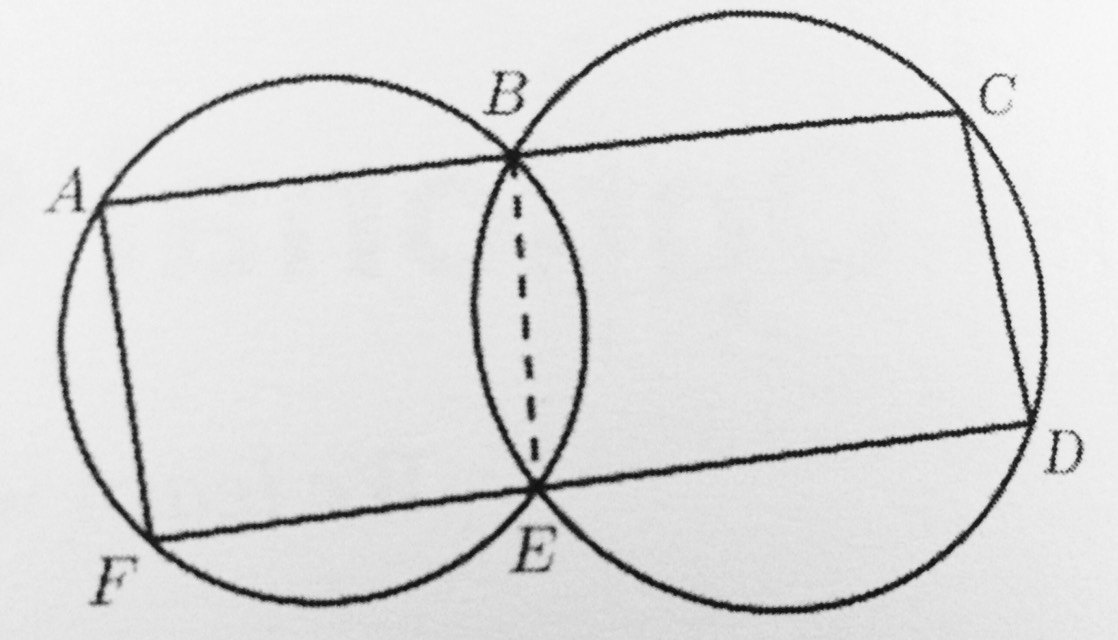
In the diagram, two circles intersect at B and E. ABC is a line parallel to the FED. How do you prove that ACDF is a parallelogram?
1 Answer
Proof: involving co-interior angles and cyclic quadrilaterals
Explanation:
Since we already know that
We're going to do this by finding expressions for the angles
Since ABC and FED, are parallel, the angles form between those and FA and CD are co-interior (also know as allied) angles.
Two co-interior angles sum to 180.
What we have here with ABEF and BCDE are cyclic quadrilaterals; since all of the sides of the quadrilaterals they form lie on the circumference of the same circle.
Opposite angles in a cyclic quadrilateral sum to 180
We now have two simultaneous equations involving
You should get this no matter which one you use.
Let
(this will make calculations from now on easier to write).
