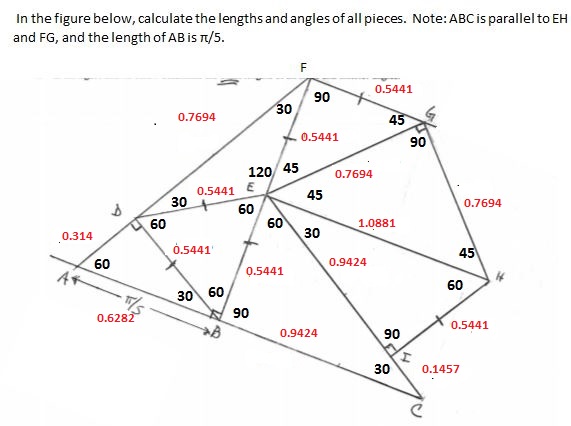
Given : #AB = pi / 5, BD = BE = DE = EF = FG= HI#
#AhatBD = 90 - 60 = 30^0# as BDE is equilateral triangle and #AhatBE = 90^0#
#B^AD = 60^0#
In triangle ABD,
#AD = AB sin 30 = (pi/5) * (1/2) = 0.314#
#BD = DE = EF = BE = HI = (pi/5) * cos 30 = 0.5441#
#AhatDB + BhatDE + EhatDF = 180#
#EhatBD = 180 - 90 - 60 = 30#
In Triangle DEF,
#EhatDF = EhatFD = 30# Isosceles triangle.
#:. DF = DE / sin 45 = 0.5441 * sqrt2 = 0.7694#
In isosceles right triangle EFG,
#FhatEG = FhatGE = (180 - EhatFG)/2 = (180 - 90)/2 = 45^0#
as FG parallel AB and #EhatFD = EhatBA = 90^0#
#EG = EF sqrt2 = 0.7255 sqrt2 = 0.7694#
Since EH and FG are parallel,
#FhatEH = EhatFG = 90^0#; but #FhatEG = 45^0#
#:. GhatEH = GhatHE = 45^0, EG = GH = 0.7694#
In triangle EGH, #EH = 0.7694 * sqrt2 = 1.0881#
In right triangle EHI,
#sin (HEI) = (HI) / (EH) = 0.5441 / 1.0881 = 1/2# or #HhatEI = 30^0#
#EhatHI = 180 - 90 - 30 = 60^0#
#EI = sqrt((EH)^2 - (HI)^2) = sqrt((1.0881)^2 - (0.5441)^2) = 1.2166#
#In triangle EBC, BhatEC = 60, BhatCE = 30# as BC parallel EH
#BC = (BE) / tan 30 = 0.5441 / (1/sqrt3) = 0.9424#
#CE = (BE) / sin 30 = 0.7255 / (1/2) = 1.0881#
As can be seen, CE - EI = HI = 1.0881 - 0.9424 = 0.1457

