In the following graph, how do you determine the value of c such that #lim_(x->c) f(x)# exists?
1 Answer
May 13, 2018
show below
Explanation:
show below:
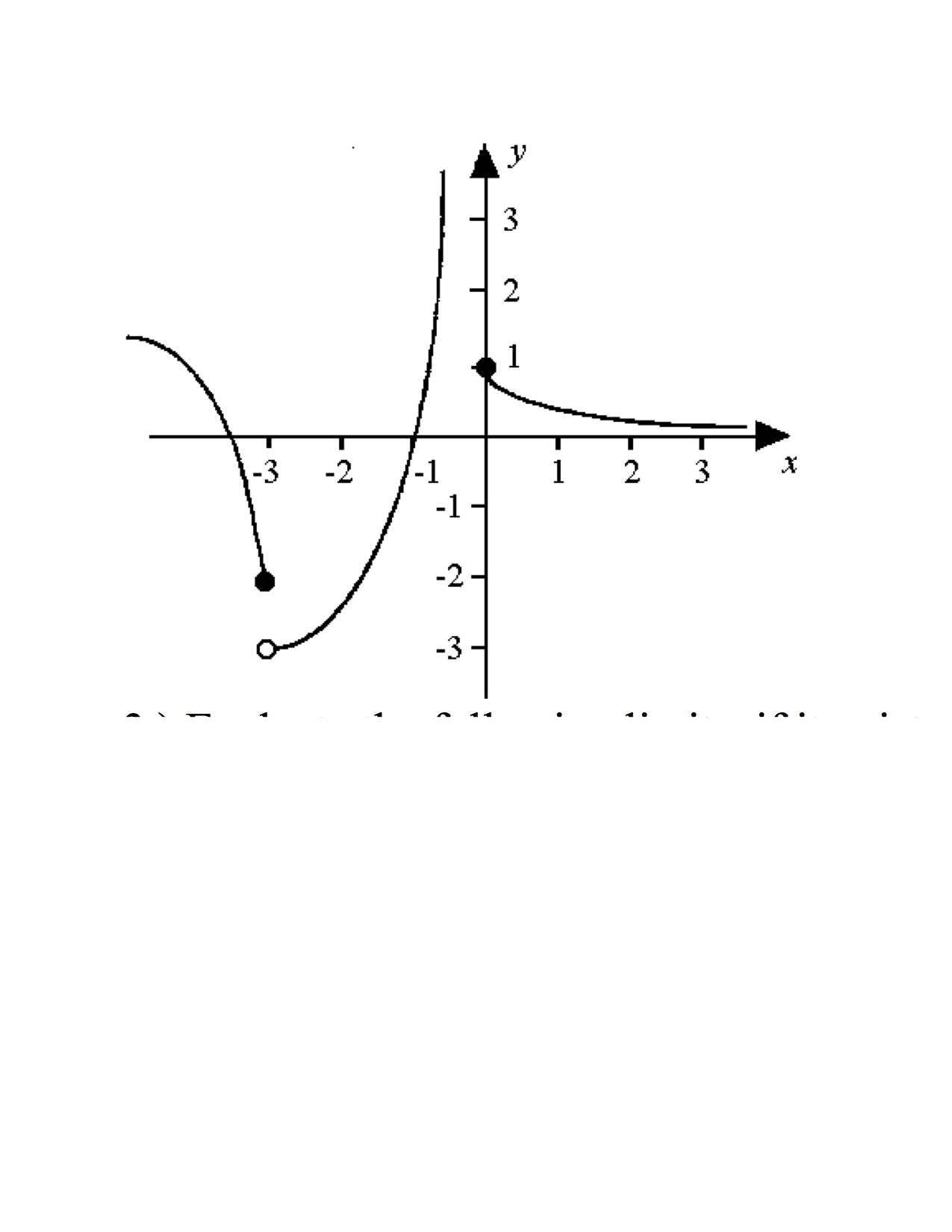
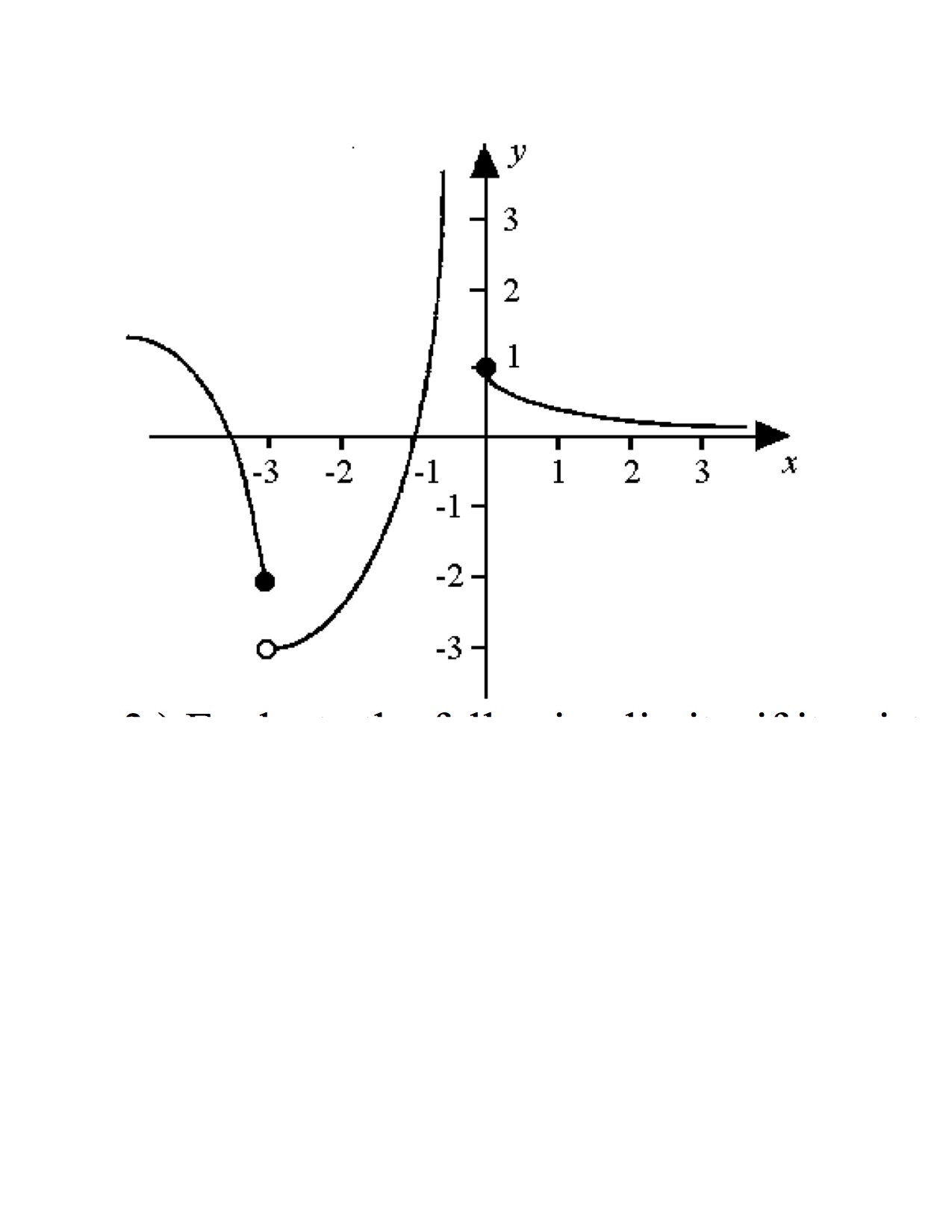
For the function in the graph below f(x) is defined when x = -2 but the value which f(x) will approach as x gets closer to -3 from the left is different from the value that it will approach as x gets closer to -3 from the right.
Looking at the graph we can see that as x approaches -3 from the left f(x) approaches (negative two) however as x approaches -3 from the right f(x) approaches (negative three).
so
the limit does not exist at
in the same way when x rarr to zero
the limit does not exist at
so the values of c equals

