Question

In triangle `ABC`, `AB=15, BC=12` and `CA=8`. What are the angles of the triangle in order from smallest to largest?

Answer 1

`B~~32.11^@`,
`A~~52.82^@`,
`C~~95.07^@`

Explanation:

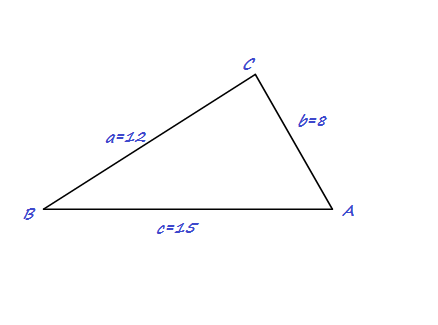
The above figure represents the `Delta ABC`,where

• `a= BC =12`

• `b= CA =8`

• `c= AB =15`

Smallest angle B is to be opposite of smallest side b.
By properties of triangle

`cosB=(c^2+a^2-b^2)/(2ca)=(15^2+12^2-8^2)/(2xx15xx12)`

`=305/360=0.847`

`B=cos^-1(0.847)~~32.11^@`

`cosA=(c^2+b^2-a^2)/(2cb)=(15^2+8^2-12^2)/(2xx15xx8)`

`=145/240=0.604`

`A=cos^-1(0.604)~~52.82^@`

`cosC=(a^2+b^2-c^2)/(2ab)=(12^2+8^2-15^2)/(2xx12xx8)`

`=-17/240=-0.0885`

`C=cos^-1(-0.0885)~~95.07^@`