.
y=f(x)=x^6-4x^5
First, we take the derivative of the function, set it equal to 0 and solve for its roots:
dy/dx=6x^5-20x^4
6x^5-20x^4=0
2x^4(3x-10)=0
x=0 with multiplicity of 4
3x-10=0, :. x=10/3
Now, we conduct the first derivative test by plugging in values of x that are slightly smaller and slightly larger than each root we found.
Because, doing this determines the slope of the tangent to the curve at each x value, if the derivative becomes positive at a point it means the function is increasing at the point. If it becomes negative it means the function is decreasing at that point.
This process determines which of the roots we found is a maximum or a minimum of the function.
By the way, because x=0 happens multiple times. It is neither a minimum nor a maximum. Rather, at that point, the function becomes tangent to the x-axis and the point is an inflection point, i.e. the function changes concavity.
Therefore, the only point that is either a maximum or a minimum is at x=10/3. Now, we need to figure out which it is. Let's pick an x value smaller than 10/3 like x=2. Let; plug it into the derivative:
dy/dx=6(2)^5-20(2)^4=6(32)-20(16)=192-320=-128
Now, let's pick an x value larger than 10/3 like 4:
dy/dx=6(4)^5-20(4)^4=6144-5120=1024
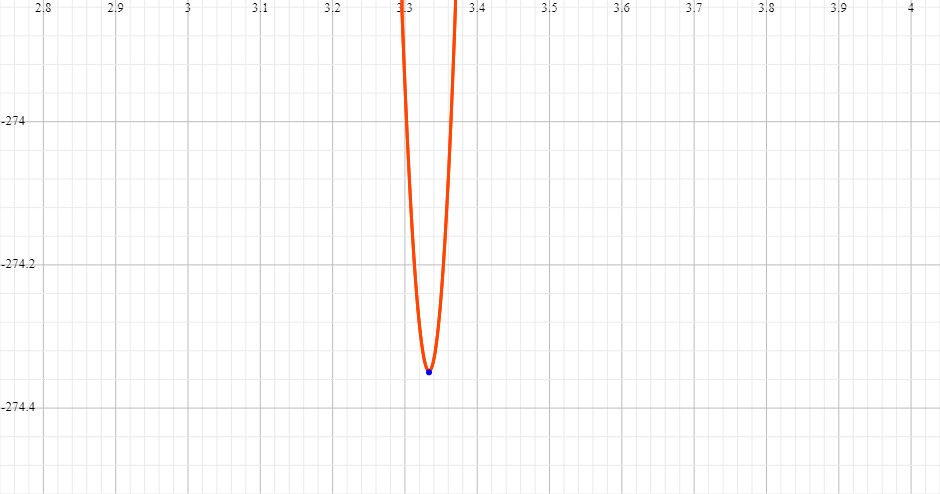
This shows that the function is decreasing before x=10/3 and increasing after it. Therefore, x=10/3 is a minimum.
Let's do the same test at x=0 to find what the function is doing before and after this point.
For x=-1:
dy/dx=6(-1)^5-20(-1)^4=-6-20=-26
For x=1:
dy/dx=6(1)^5-20(1)^4=6-20=-14
This shows that the function is decreasing both before and after x=0.
As such, the answer to the first part of the question is:
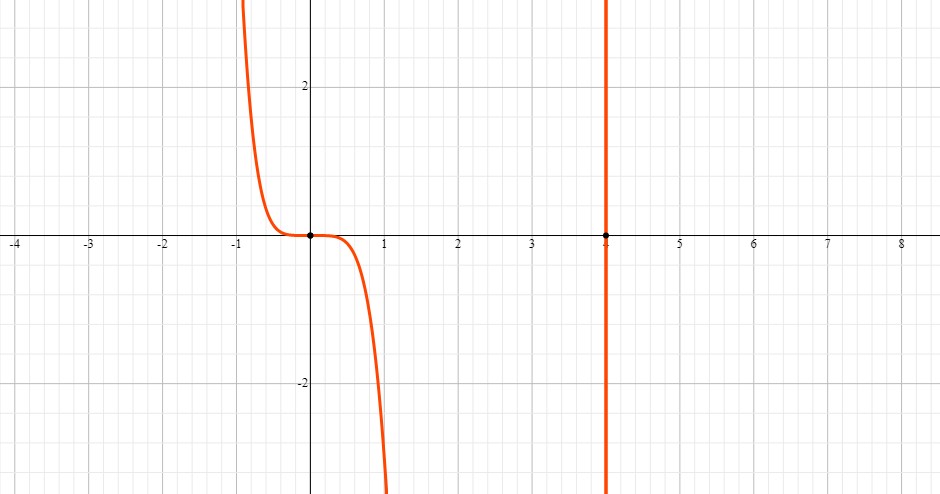
-oo < x < 10/3 is the region where the function is decreasing.
10/3 < x < oo is the region where the function is increasing.
Now, we take the second derivative of the function, set it equal to 0, and solve for its roots:
(d^2y)/dx^2=30x^4-80x^3
10x^3(3x-8)=0
x=0 and 8/3
These are the inflection points. We have to conduct the second derivative test to find whether the function is concave up or down before and after each of these points.
x=-1, :, (d^2y)/(dx^2)=30(-1)^4-80(-1)^3=30+80=110
x=1, :. (d^2y)/(dx^2)=30(1)^4-80(1)^3=30-80=-50
x=2, :. (d^2y)/(dx^2)=30(2)^4-80(2)^3=480-640=-160
x=3, :. (d^2y)/(dx^2)=30(3)^4-80(3)^3=2430-2160=270
The above results show that:
-oo < x < 0 and 8/3 < x < oo are the regions where the function is concave up.
0 < x < 8/3 is the region where the function is concave down.
All of this can be seen in the graph below:
Here is the bottom part of the graph where the minimum is: