int_0^pi max(sin(x),cos(x)) dx =?
3 Answers
Apr 12, 2017
Assuming I've read the expression correctly:
Explanation:
So
Apr 12, 2017
Explanation:
I get
Explanation:
Here are the graphs of sine (red) and cosine (blue).
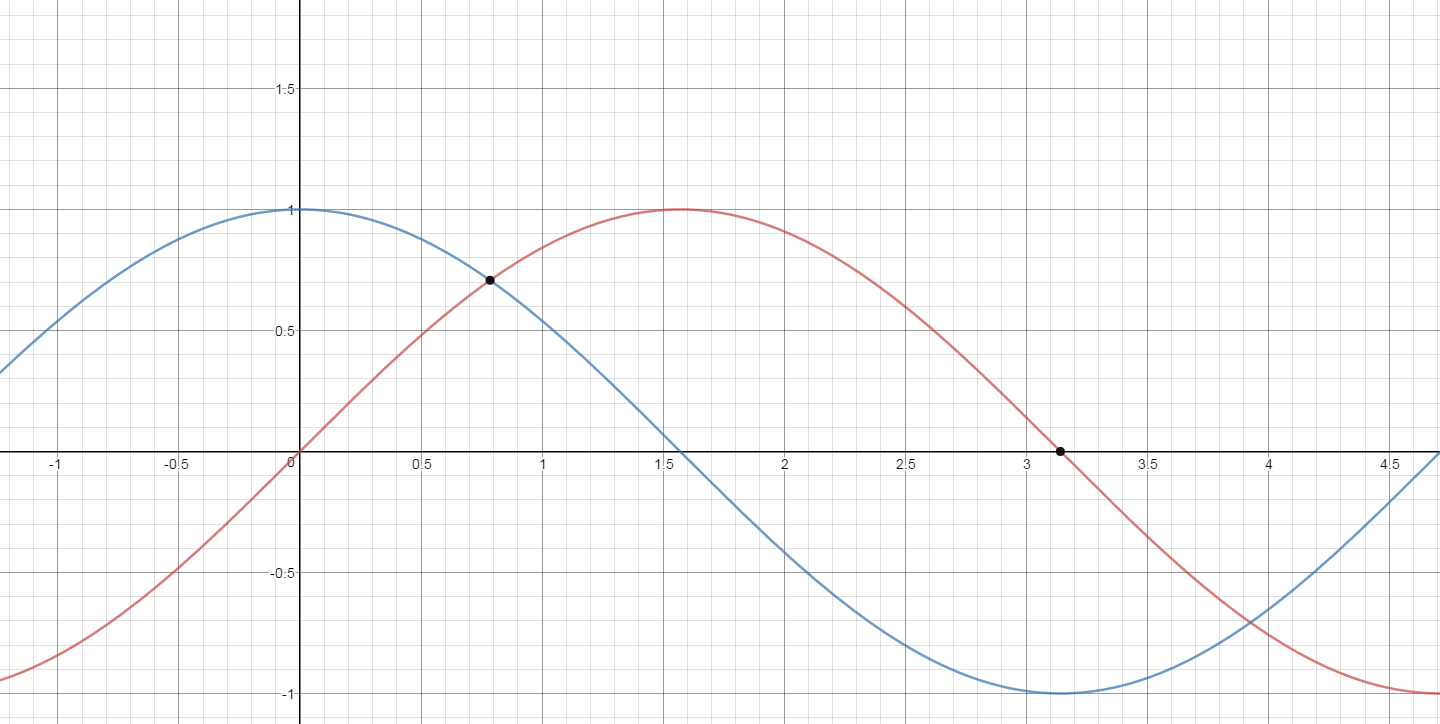
On
Therefore,
= [sqrt2/2]+[1+sqrt2/2] = 1+sqrt2



