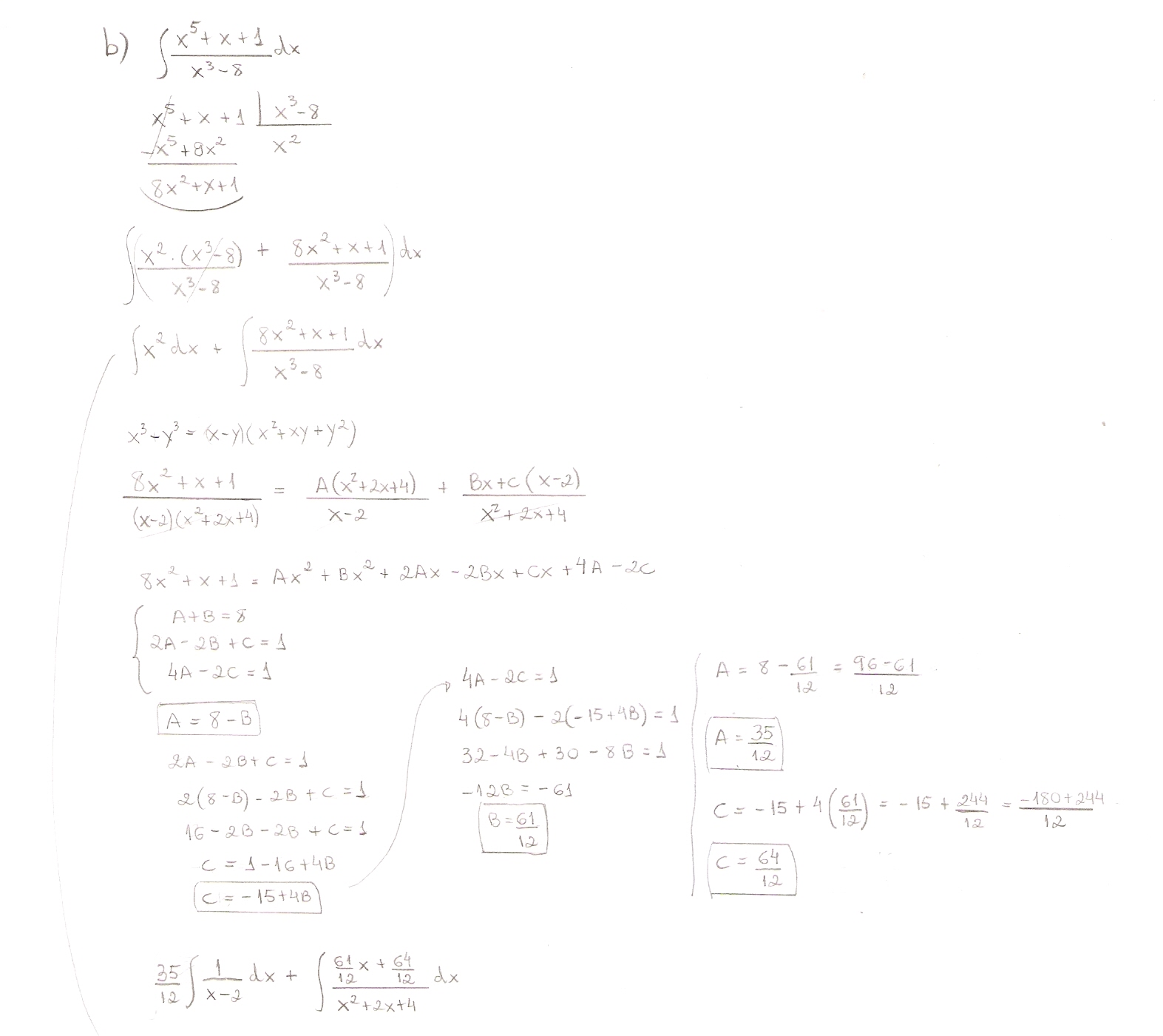You have done almost all the heavy lifting here! The first of the two integrals is really simple,
#35/12int 1/(x-2) dx = 35/12 ln|x-2|#
so I am guessing you need help with the second:
#1/12 int (61x+64)/(x^2+2x+4) dx#
For this, note that
#d(x^2+2x+4)=(2x+2)dx=2(x+1)dx#
so that it makes sense to split up the numerator into
#61x+64=61(x+1)+3#
Then
#1/12 int (61x+64)/(x^2+2x+4)dx=61/12 int (x+1)/(x^2+2x+4)dx +1/12 int 3/(x^2+2x+4)dx#
The first of these is
#61/24 int (2(x+1)dx)/(x^2+2x+4) =61/24 ln(x^2+2x+4)#
while the second is
#1/4 int (dx)/(x^2+2x+4) = 1/4 int dx/((x+1)^2+3) = 1/(4sqrt3) tan^-1((x+1)/sqrt3)#
Adding all the terms (including the #int x^2 dx#) we get the integral :
#x^3/3+35/12 ln|x-2|+61/24 ln(x^2+2x+4)+1/(4sqrt3)tan^-1((x+1)/sqrt3)+C#