Question

Integration of sinx/x from 0 to infinity?

Answer 1

`int_0^oo \ sinx/x \ dx = pi/2`

Explanation:

We seek:

`I = int_0^oo \ sinx/x \ dx`

Let `g(x) = sinx/x => g(-x) = sin(-x)/(-x) = sinx/x`

Thus `g(x)` is an even function, and as such:

`2I = int_(-oo)^oo \ sinx/x \ dx`

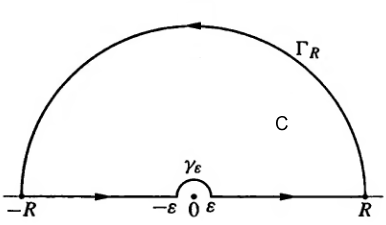
Consider the complex based function `f(z)=e^(iz)/z`, Which has a simple pole at `z=0`, we then consider the contour integral:

`J = oint_C \ f(z) \ dz = oint_C \ e^(iz)/z \ dz` where `z in CC`

Where `C` is a semicircle of radius `R` centred at the origin that is deformed at the origin with a smaller semicircle of radius `epsilon` to excludes the pole at `z = 0`, and we traverse the contour in an anticlockwise direction.

The integrand has no poles in `C` as the pole `z = 0` is excluded in the above construction. Thus, by Cauchy’s Theorem:

`oint_C \ f(z) \ dz = 0`

Now (in shorthand),

`oint_C \ f(z) \ dz = int_(-R)^(epsilon) + int_(gamma_epsilon) + int_(epsilon)^R + int_(Gamma_R) = 0`

We require an estimate for `int_(Gamma_R) \ f(z) \ dz`. Noting that `z=Re^(i theta)` on `Gamma_R`, we have:

`abs(int_(Gamma_R) \ e^(iz)/z \ dz) = abs(int_o^oo \ e^(iRcos theta-R sin theta) / (Re^(i theta)) iRe^(i theta) \ d theta )`
`" " le int_0^pi e^(-Rsin theta) \ d theta`
`" " = 2 int_0^(pi/2) e^(-Rsin theta) \ d theta`
`" " le 2 int_0^(pi/2) e^((-2R theta) / pi) \ d theta \ \ \ \` using `sin theta ge (2theta)/pi`
`" " = 2 [ (2e^((-2Rtheta)/pi) )/ ((-2R)/pi) ]_0^(pi/2)`
`" " = pi/R(1-e^-R)`
`" " rarr 0` as `R rarr oo`

Given that the small circle `gamma_epsilon` has the equation `z = r(cos theta + isin theta)` for `theta:pi rarr 0` then

`lim_(epsilon rarr 0) int_(gamma_epsilon) \ f(z) \ dz = i \ lim_(epsilon rarr 0) int_pi^0 \ e^(-rsin theta)e^(ircos theta) \ dz`
`" " = -pi i`

Taking the two limits `R rarr oo` and `epsilon rarr 0`, and combining all these results, we have:

`int_(-oo)^oo e^(iz)/z \ dz - pi i = 0 => int_(-oo)^oo (cosx+isinx)/x \ dx = pi i`

Equating real and imaginary coefficients we get:

`Re: int_(-oo)^oo cosx/x \ dx = 0`
`Im: int_(-oo)^oo sinx/x \ dx = pi`

Then using the initial result

`2I = int_(-oo)^oo \ sinx/x \ dx => 2I = pi`

Hence,

`I = pi/2`