For #A={(x,y)inRR^2; 0<=y<=3, x/10<=y<=x}#
#intint_Asqrt(xy-y^2)dxdy = int_{y=0}^3(int_{x=y}^{10y}sqrt(xy-y^2)dx)dy#
#qquad = int_{y=0}^3(2/(3y)(xy-y^2)^(3/2))_{x=y}^{10y}dy#
#qquad = int_{y=0}^3[2/(3y)(10y^2-y^2)^(3/2)-2/(3y)(y^2-y^2)^(3/2)]dy#
#qquad = 2/3int_{y=0}^3 27y^2dy=2/3 times 27/3(3^3-0^3)=162#
To get some geometric intuition into this, let us take a look at this graphically. The region #A# is shown shaded below :
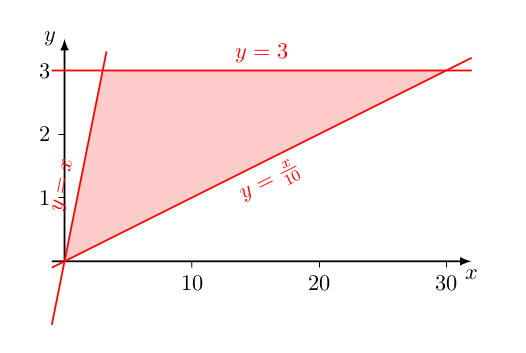
The double integral actually means "breaking up" this region into tiny pieces (like the darkened rectangle #dx\ dy# in the picture below) and summing up the integrand times the area over all such pieces.
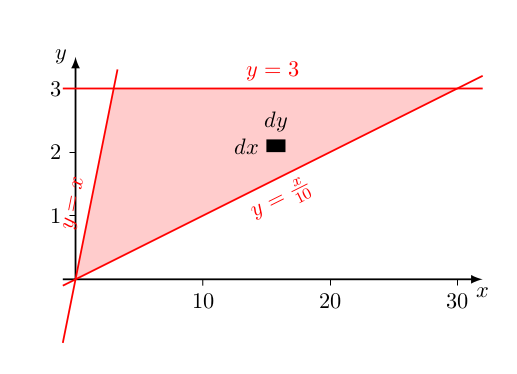
We can decide to either integrate over #x# first, which essentially means adding up over all rectangular pieces at the same #y# to get the contribution from the horizontal strip shown below :
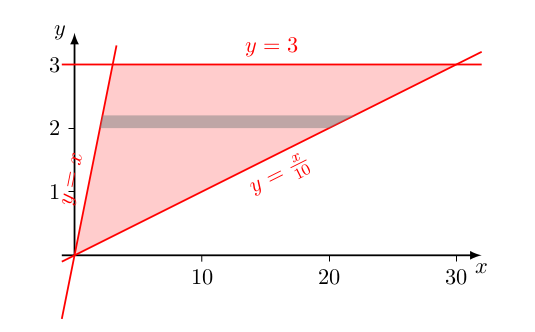
The limits for this integration is decided by how much #x# can vary at this fixed value of #x#. From the geometry, it is clear that #x# varies from #y# to #10y# - hence the limits.
We now integrate over #y#, This means summing up over all the horizontal strips, from #y=0# to #y=3# :
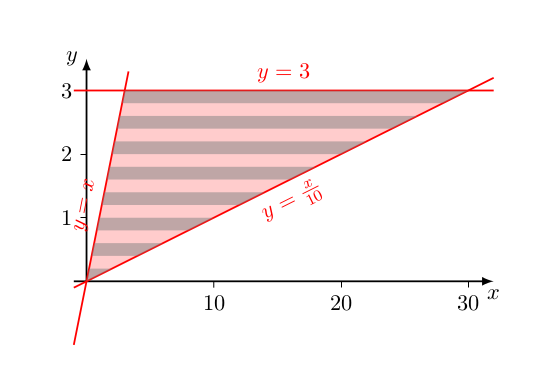
You could have decided to integrate over #y# first , so that you would have vertical strips first, which are then added over.Let me leave this as an exercise!





