Is delta G zero at boiling point?
1 Answer
Yes, it is. At the boiling point,
For a proof of this, look below.
Take a look at this diagram:
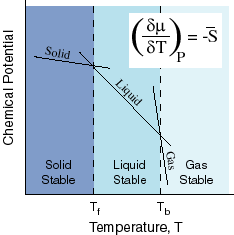
where
#mu = barG = G/n# ;
#mu = # Chemical Potential (like high and low energy states)#G = # Gibbs' Free Energy#barG = # Molar Gibbs' Free Energy#S = # Entropy#barS = # Molar Entropy#n = # moles
This graph basically says, within each particular phase, the negative change in Gibbs' Free Energy per mole of substance as the temperature changes at a constant pressure is equal to the entropy per mole of substance. This can be written as:
#\mathbf(-((delmu)/(delT))_P = -((delbarG)/(delT))_P = barS)#
or
#-n((delmu)/(delT))_P = -((delG)/(delT))_P = S#
On this graph, outside of phase changes, the pressure is assumed to be constant within a particular phase (that's what the subscript P means) but the temperature is not (
At the boiling point, you're at
Let us write out the following Maxwell relation:
#DeltaH = TDeltaS + VDeltaP#
or the differential form
#\mathbf(dH = TdS + VdP)# where
#H# is enthalpy,#V# is volume, and#P# is pressure, we can see that enthalpy depends on temperature, pressure, and entropy (entropy is not constant in a phase change since the moving particles are starting to change speed due to the change in volume).
When the temperature is constant but the pressure is not constant, this relationship holds true as-is. Since pressure is constant, we can eliminate
#dH = TdS + cancel(VdP)#
Thus, integrating with respect to entropy at a constant temperature, we get:
#DeltaH_(vap) = T_(vap) int_(S_1)^(S_2) dS = T_(vap)DeltaS_(vap)#
But wait, that means...
#DeltaH_(vap) - T_(vap)DeltaS_(vap) = 0#
#DeltaG_(vap) = cancel(DeltaH_(vap) - T_(vap)DeltaS_(vap))#
#color(blue)(DeltaG_(vap) = 0)#
So yes,

