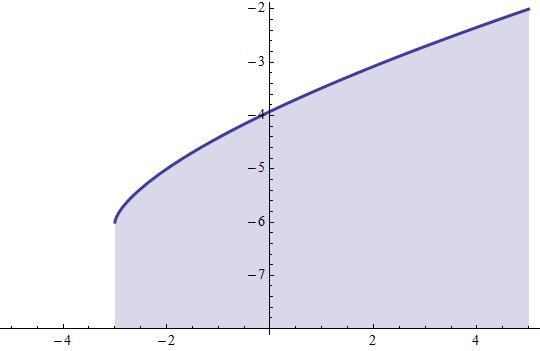
For #x in (-3,oo)# as we can see, #f(x) = (x+3)^(2/3) - 6# has a convex hypograph. This can be stated observing that in the same range, #f'(x) =2/(3 (3 + x)^(1/3)) # has a positive strictly decreasing value. Further rigorous proof can be established by stating that if
#(x_1,f(x_1))# and #(x_2,f(x_2))# are two hypograph points, then
#(x_1+lambda(x_2-x_1),f(x_1+lambda(x_2-x_1)))# for #lambda in [0,1]# is also a hypograph point.
Attached the hypograph set