Is my teacher's final answer wrong?
Hi, for iii) my teacher got x = -2.. however I got x = 2.. if my teacher is correct, how did he get x = -2.. since the math shown kinda skips through that part..

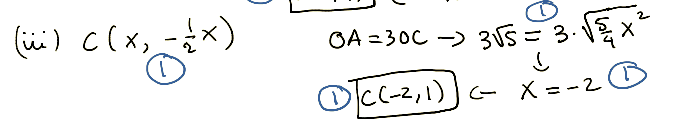
Hi, for iii) my teacher got x = -2.. however I got x = 2.. if my teacher is correct, how did he get x = -2.. since the math shown kinda skips through that part..

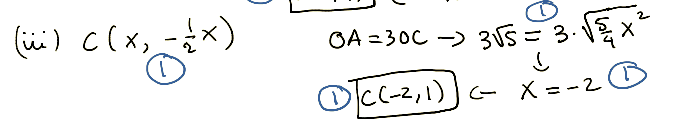
1 Answer
Your teacher is correct...
Just note that I worked through all the parts to help you catch your mistake.
Explanation:
Let's find the slope from points
Just note here that the slop is also the slope from
Since
Since line
Also, since the triangle
If we set this as our base, then our hight is
This is the length of
We can get two equations from this:
Let the coordinates of point
We can come up with the following:
We also use the distance formula using the fact that the length of segment
We also know
Now, the important part:
We know the distance from
Using our information from the problem, we know that the distance from
We also know that the slope from
Since the line intersects at the origin, the slope is the
Therefore,
Using our information, we have:
Therefore,

