Is the following solution correct? If not, why?

Question

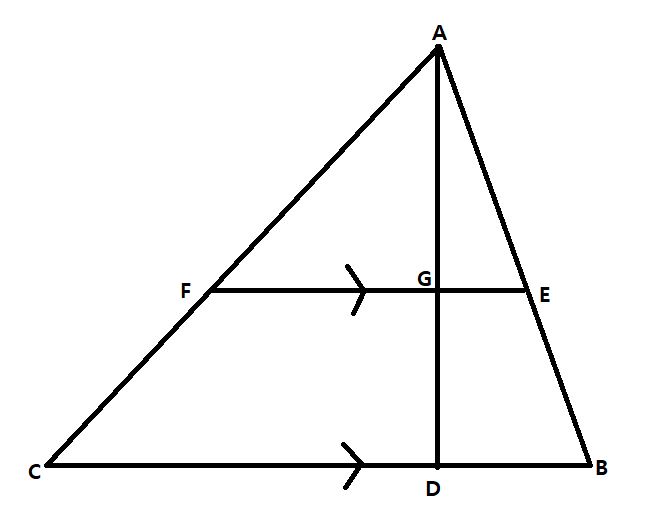
The problem: A line parallel to the base of a triangle cuts the triangle into two regions of equal area. This line also cuts the altitude into two parts. Find the ratio of #(GD)/(AG)#

Solution:

#[[ABC]]/[[AEF]]=((AD)/(AG))^2#

#=>2=((AG+GD)/(AG))^2#

#=>sqrt2=(AG+GD)/(AG)#

#=>sqrt2=1+(GD)/(AG)#

#=>sqrt2-1=(GD)/(AG)#

1306 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-05T15:52:02

The answer is #=sqrt2-1#

The areas of #" triangle AFE"# and #"trapezium " CFEB# are equal.

#1/2*FE*AG=1/2(CB+FE)*GD#

Therefore,

#(GD)/(AG)=(FE)/(CB+FE)=1/(1+((CB)/(FE)))#...........#(1)#

The area of #" triangle AFE"# is half the area of #"triangle " ACB#

#1/2*FE*AG=1/2*1/2CB*AD# .

#FE*AG=1/2CB*AD#

#(CB)/(FE)=2*(AG)/(AD)#

But #AD=AG+GD#

Therefore

#(CB)/(FE)=2*(AG)/(AG+GD)#

#(CB)/(FE)=2/(1+(GD)/(AG))#

Substituting this value in equation #(1)#

#(GD)/(AG)=1/(1+(2/(1+(GD)/(AG)))#

Let #(GD)/(AG)=x#

Then,

#x=1/(1+(2/(1+x))#

#=>#, #x=(1+x)/(3+x)#

#=>#, #x(3+x)=1+x#

#=>#, #x^2+3x=1+x#

#=>#, #x^2+2x-1=0#

Solving this quadratic equation

#x=(-2+-sqrt(4-4(-1)(1)))/(2)#

#=(-2+-sqrt8)/(2)#

#=(-1+-sqrt2)#

We keep only the positive value

#(GD)/(AG)=sqrt2-1#