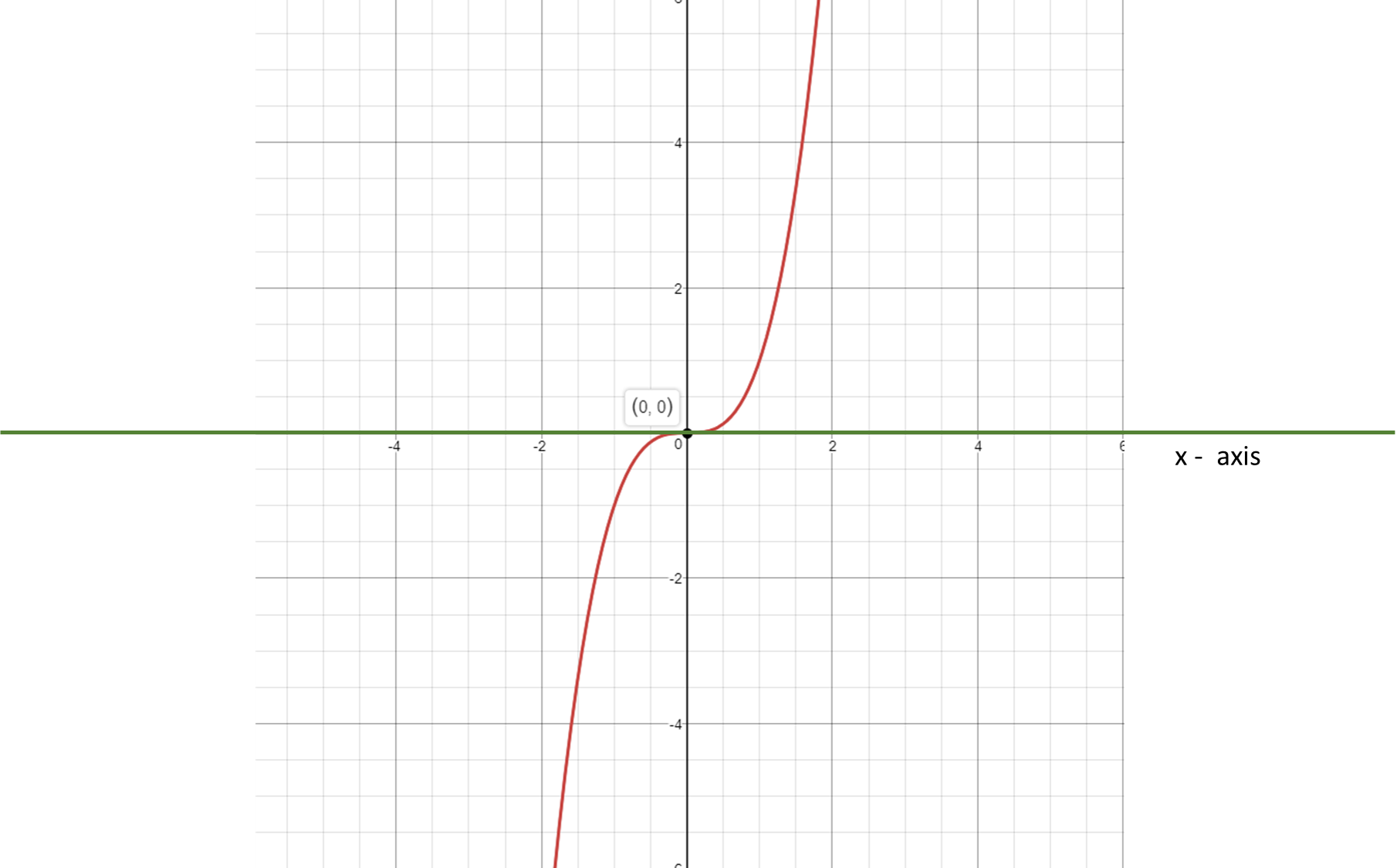
Is the x-axis tangent to #y = x^3#?

Question

8538 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-08T06:04:07

Since the slope of the curve is zero at #x=0# where the curve
cuts the x-axis, x-axis is tangent to the given curve.

Given =

#y=x^3#

This curve passes through origin #x=0#.
The slope of the X-axis is zero.

The slope of the given curve at any point is #dy/dx=3x^2#

The slope of the curve at #x=0# is #m=3(0)^2=0#

Since the slope of the curve is zero at #x=0# where the curve
cuts the x-axis, x-axis is tangent to the given curve.

enter image source here