Question

Is there a formula for kinetic theory of gases (the collision with a wall)? If there is, how can I derive it?

How can I show the basic steps how that formula was made?

Answer 1

Consider a hard-sphere model for an ideal gas (call it molecule 1) traveling at velocity `u_(1x)` towards a wall of area `A = bc` (with `a ne b ne c`):

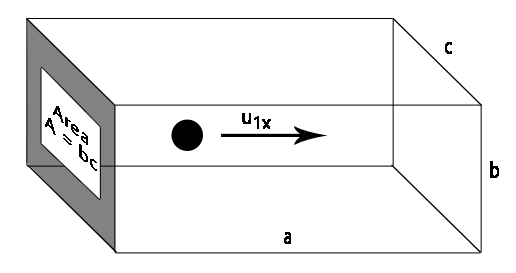
The momentum of the particle is then `p_(ix) = m u_(1x)`.

Exactly when the particle collides with the wall, we assume the collision is elastic (no kinetic energy is lost), and that the new momentum after hitting the wall becomes `p_(fx) = -m u_(1x)`.

Therefore, the change in momentum over time, starting at the moment the particle hits the rear wall and bounces back, hits the front wall, and returns to the rear wall without colliding again, becomes:

`(Deltap_x)/(Deltat) = (Delta(m u_(1x)))/(Deltat) = (m u_(1x) - (-m u_(1x)))/(Deltat)`

The velocity was

`u_(1x) = (2a)/(Deltat)`,

so that `Deltat = (2a)/(u_(1x)`. So:

`=> (2m u_(1x))/(2a"/"u_(1x)) = (m u_(1x)^2)/a`

Recall that `int F_xdt = p_x`, where `F_x` is the force in the `x` direction. Therefore, the force exerted by molecule 1 on the rear wall is `F_1`:

`(Deltap_x)/(Deltat) = F_1 = (m u_(1x)^2)/a`

Also recall that the pressure exerted on the rear wall is `P = F/A`, so:

`P_1 = F_1/(bc) = (m u_(1x)^2)/(abc) = (m u_(1x)^2)/V`,

where `V = abc` is the volume of the container.

When we expand this expression to consider all molecules colliding with the same wall, we obtain:

`P = sum_(j=1)^(N) P_j = sum_(j = 1)^(N) (m u_(jx)^2)/V = m/V sum_(j=1)^(N) u_(jx)^2`

where `N` is the total number of molecules.

Note that `1/N sum_(j=1)^(N) u_(jx)^2 = << u_x^2 >>`, the average value of `u_x^2` (the expectation value). Therefore, we can plug in this expression to obtain:

`P = m/V sum_(j=1)^(N) u_(jx)^2 = m/V N * 1/N sum_(j=1)^(N) u_(jx)^2`

`=> PV = Nm<< u_x^2 >>`

Although we chose the x direction in the derivation, we could have chosen any arbitrary direction (a homogeneous gas is "isotropic"; it has the same properties in any direction).

So, `<< u_x^2 >> = << u_y^2 >> = << u_z^2 >>`. The total speed `u` of any molecule is

`u^2 = u_x^2 + u_y^2 + u_z^2`,

so the average value of the total speed squared is then:

`<< u^2 >> = << u_x^2 >> + << u_y^2 >> + << u_z^2 >>`

Therefore, since the averages of the squared speed in each dimension are all equal, if we average the three average squared speeds in each dimension, we get the average of the squared speed in any arbitrary direction, `<< u^2 >>`.

`=> color(blue)(PV = 1/3 N m << u^2 >>)`

Lastly, note that `sqrt(<< u^2 >>)` is called the root-mean-square speed, `u_(RMS)`.