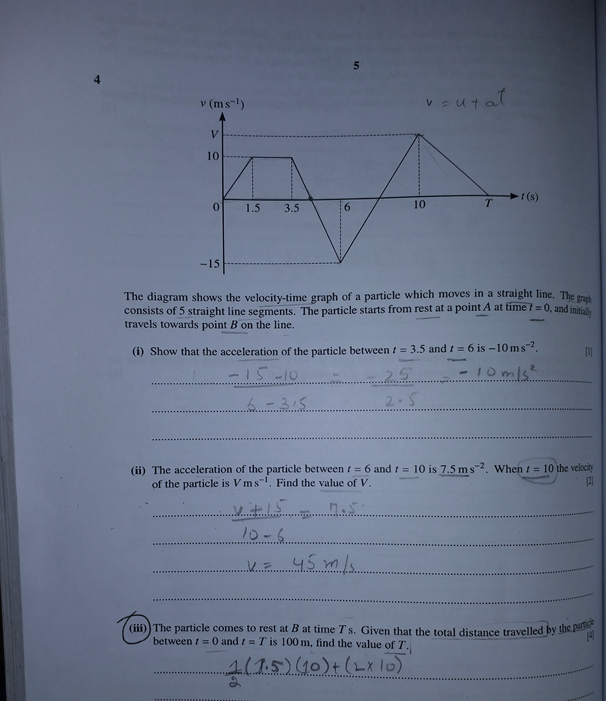
It is question about finding distance from velocity time graph?

enter image source here

3 Answers
Somebody N.
Apr 27, 2018

See below.

Explanation:

If you have a graph of velocity against time, the area under the graph represents the distance.

This makes sense if you consider this:

#"Distance"="velocity"xx"time"#

On the graph:

Distance along t axis x distance along v axis.

You can find the area if it linear by using areas of squares, rectangles, trapeziums etc.

A08
Apr 28, 2018

This is what I get

Explanation:

Let us start with Part
(ii) We need to use kinematic expression

#v=u+at#

Inserting given values

#V=-15+7.5xx(10-6)#
#=>V=-15+30=15\ ms^-1#

(iii)

  1. Area of trapezoid #=1/2("sum of parallel bases")xx"height"#
    Length of top base #=3.5-1.5=2\ s#
    To calculate length of lower base we need to find time #t_1# when velocity becomes #=0#. Counting time from #t=3.5\ s#
    From the information given in (i)

    #0=10+(-10)xxt_1#
    #=>t_1=1\ s#
    #:.# Length of lower base#=3.5+1=4.5\ s#
    Now Area of trapezoid #=1/2(2+4.5)xx10=32.5\ m#

  2. Area of first triangle #=1/2"base"xx"height"#
    To calculate length of base we need to find time #t_2# when velocity becomes #=0#. Counting time from #t=6\ s#
    From the information given in (ii)

    #0=-15+7.5xxt_2#
    #=>t_2=2\ s#
    #:.# Length of base #=# Time gap between two instances when velocity becomes zero#=8-4.5=3.5\ s#
    Area of first triangle #=1/2xx3.5xx|-15|=26.25\ m#
    We have taken the magnitude of velocity as we need to find distance which is a scalar quantity.
    (if we take negative sign in consideration we will get displacement which is a vector quantity)

  3. From the given and calculated values
    Total distance #=100=#Area of trapezoid#+#Area of first triangle#+#Area of second triangle
    #=>100=32.5+26.25+#Area of second triangle
    #=>#Area of second triangle#=41.25\ m#
    #41.25=1/2"base"xx"height"#
    #=>41.25=1/2"base"xx15#
    #=>"base"=41.25xx2/15=5.5\ s#
    #:.T=8+5.5=13.5\ s#
Somebody N.
Apr 28, 2018

#T=13.5\ s#

Explanation:

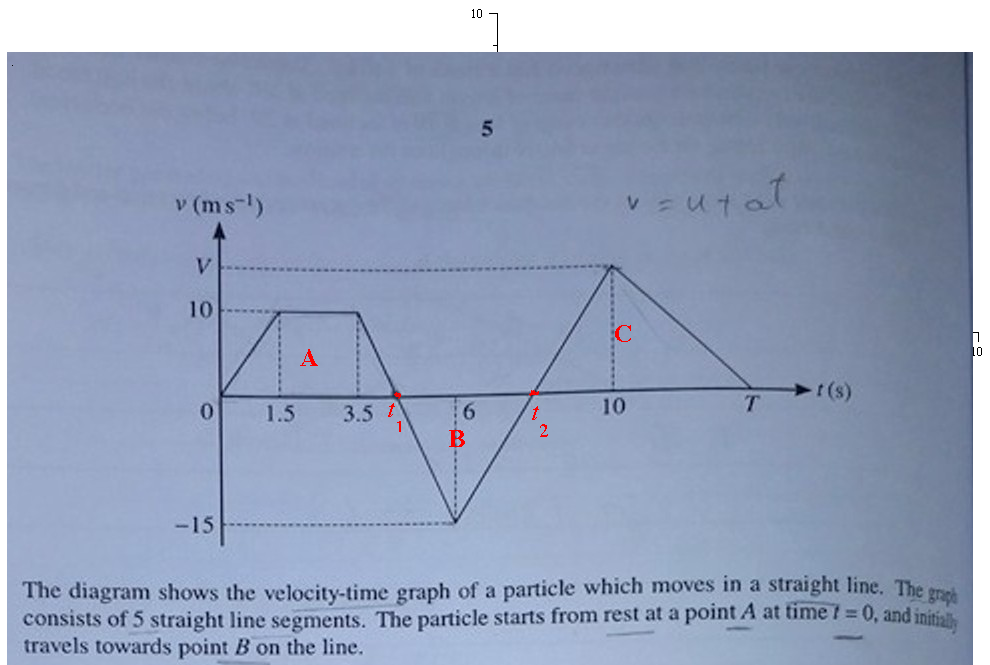
enter image source here

For question (ii), you have made an error.

Using #v=u+at#

Initial velocity #= -15ms^(-1)# #color(red)("at" \ \ \t=6)#

Acceleration #= 7.5ms^(-2)#

#t=10-6=4#

#v=-15+7.5(4)=15ms^(-1)#

Question (iii).

We need to find areas A , B, C

In order to do this we first need to find #t_1 and t_2#

For #t_1#

From question (i) we are told acceleration between 3.5 and 6 is #-10ms^(-1)#

Using # \ \ \ \v=u+at#

Velocity is zero at #t_1#

Velocity is #10ms^(-1)# at #t=3.5#

#:.#

#0=10-10(t_1-3.5)#

#0=10-10t_1+35#

#-45=-10t_1=>t_1=color(blue)(4.5)#

For #t_2#

We know from (ii), that the acceleration between #t=6 and t=10# is #7.5ms^(-2)#

Velocity at #t=10# is #15ms^-1# ( we found this before for (ii))

Velocity at #t_2=0#

Using #v=u+at#

#15=0+7.5(10-t_2)#

#15/7.5=10-t_2#

#t_2=color(blue)(8)#

Area of trapezium (trapezoid) A

#A=1/2(t_1+(3.5-1.5))(10)#

#A=1/2(4.5+2)(10)=32.5m^2#

Area of triangle B

#1/2(t_2-t_1)(15)#

#1/2(3.5)(15)=26.25m^2#

Area of triangle C

#1/2(T-t_2)(10)#

#1/2(T-8)(15)#

#7.5T-60m^2#

The sum of these areas is #100#

#:.#

#32.5+26.25+7.5T-60=100#

Solving for T:

#T=13.5 \ s#

Related questions
Impact of this question
6259 views around the world
You can reuse this answer
Creative Commons License