It's a geometry question stating to find the area of quadrilateral ABCD?

2 Answers
Area of Quadrilateral ABCD
Explanation:
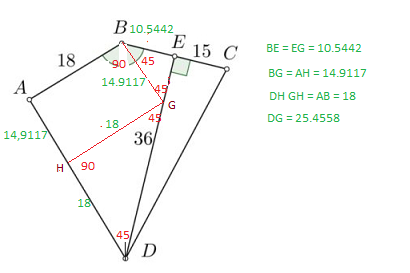
ABED is a cyclic quafrilateral as
Therefore,
Construction :
Complete rectangle ABGH with sides AB = GH = 18.
Consider isosceles Triangle BEG.
Consider isosceles triangle DGH
Area of Delta
Similarly, Area of
Area of
Consider rectangle ABGH
Area of rectangle ABGH
Area of quadrilateral ABCD is
Explanation:
.
We can add line
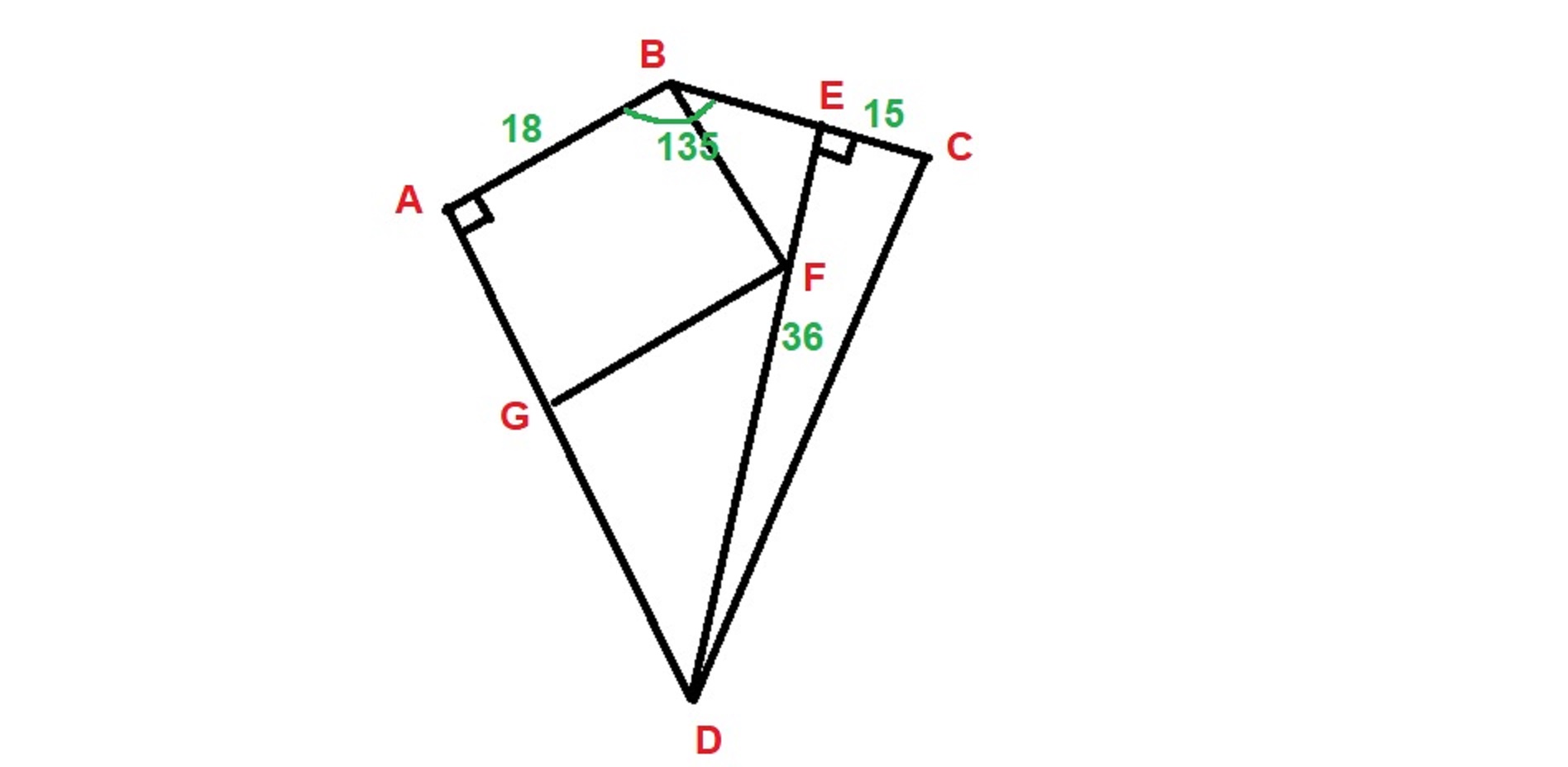
Since the sum of the angles in any quadrilateral is
Quadrilateral
Triangle
We can use Pythagoras' formula in this triangle to find the measure of
Triangle
Area of rectangle
Area of triangle
Area of triangle
Area of triangle
Area of quadrilateral

