It takes #7.21 * 10^-19# #J# of energy to remove an electron from an iron atom. What is the maximum wavelength of light that can do this?
1 Answer
Explanation:
The idea here is that the energy of a photon is proportional to its frequency.
Simply put, photons that have a high frequency will also have a high energy.
Mathematically, this relationship between the energy of a photon and its frequency is described by the Planck - Einstein equation
#color(blue)(|bar(ul(color(white)(a/a)E = h * nucolor(white)(a/a)|)))" "# . where
Now, notice that the problem is asking you for the wavelength of the photon. As you know, frequency and wavelength have an Inverse relationship described by the equation
#color(blue)(|bar(ul(color(white)(a/a)nu * lamda = c color(white)(a/a)|)))" "# , where
So, this relationship tells you that long wavelengths are associated with low frequencies, and short wavelengths are associated with high frequencies.
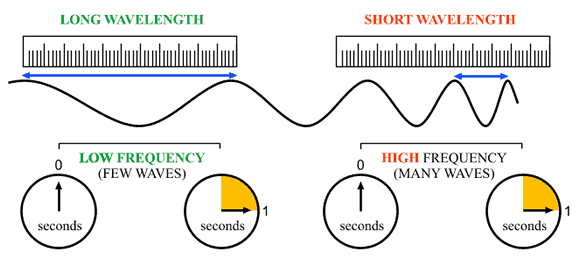
This means that a maximum wavelength of light implies a minimum frequency, which in turn implies a minimum energy associated with the photon.
You will have
#nu * lamda = c implies nu = c/(lamda)#
Plug this into the Planck - Einstein equation to get
#E = h * c/(lamda)#
Rearrange to solve for
#lamda = (h * c)/E#
#lamda = (6.626 * 10^(-34)color(red)(cancel(color(black)("J")))color(red)(cancel(color(black)("s"))) * 3 * 10^8"m" color(red)(cancel(color(black)("s"^(-1)))))/(7.21 * 10^(-19)color(red)(cancel(color(black)("J")))) = 2.76 * 10^(-7)"m"#
If you want, you can express this value in nanometers by using the conversion factor
#"1 m" = 10^9"nm"#
The answer will thus be
#lamda = color(green)(|bar(ul(color(white)(a/a)"276 nm"color(white)(a/a)|)))#
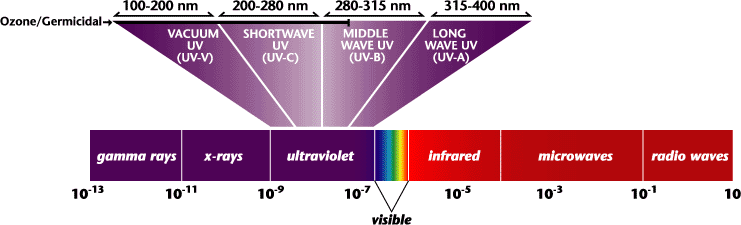
This wavelength places you in the ultraviolet - shortwave UV region of the EM spectrum.