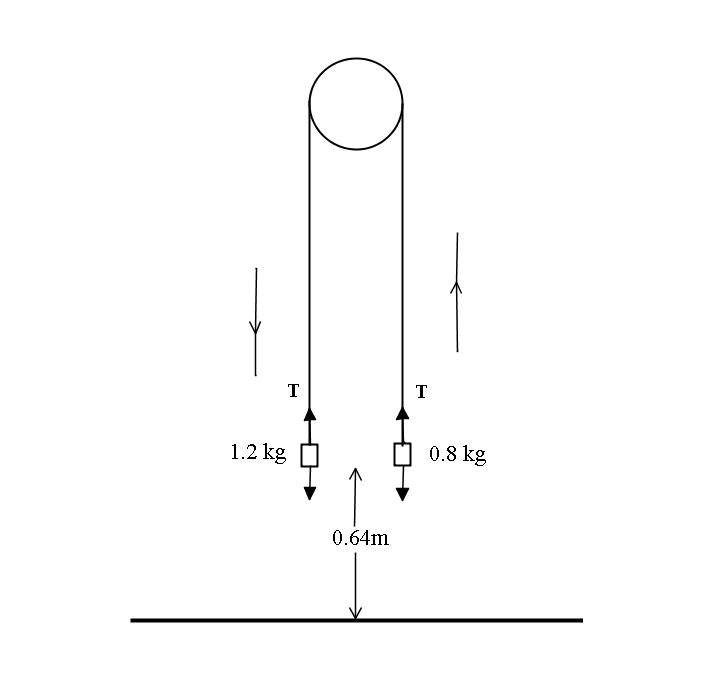
Note:
T = "string tension", we don't need to calculate this.
First find mg
1.2g and 0.8g
Don't evaluate g
Using F=ma
Write down the resultant force in the direction of motion for each particle.
1.2g-T=1.2a [1]
T-0.8g=0.8a [2]
Solve simultaneously:
Adding [1] and [2]
1.2g-0.8g=1.2a+0.8a
0.4g=2a
a=(0.4g)/(2)=0.2gms^(-2)
Now we know the rate of acceleration, we can find the distance travelled in 1 second.
Using:
S=ut+1/2at^2
Initial velocity is zero.
u=0
S=(0)1+1/2(0.2g)(1)^2
S=0.1g
g=9.81
S=(0.1)(9.81)=0.981m
From this we can see that, when the 1.2kg mass reaches the floor, the 0.8kg mass will stop accelerating, but will continue to travel upwards until gravity stops it.
We now need to find the time it takes the 1.2kg mass to travel the distance 0.64m, and consequently this will be the time the 0.8kg mass is accelerating upwards. The remaining time will be the duration the 0.8kg mass is decelerating and we need to find the distance travelled during this period.
Duration of time 1.2kg mass takes to travel 0.64m
Using:
s=ut+1/2at^2
0.64=(0)t+1/2(0.2g)t^2=>t=sqrt((1.28)/(0.2g)
g=9.81
:.
t=sqrt((1.28)/(0.2(9.81)))=0.8077100438s=0.808s 3 d.p.
Next the velocity of the 0.8kg mass after this time:
Using:
v=u+at
v=0+(0.2g)(0.808)=>v=0.1616g=1.585296 \ \ms^(-1)
Remaining time in which it decelerates due to gravity.
t=1-0.808=0.192s
Distance travelled during this period.
Using:
v^2=u^2+2as
(0)^2=(1.585)^2+2(-g)s
s=(0^2-(1.585)^2)/(2*(-g))=0.128044m
To get total distance travelled by the 0.8kg mass, we add:
0.64m+0.128044m=0.768044m
This is as close as I can get to 0.776m. This could be due to rounding errors.