Jake leaned a 12-foot ladder against his house. If the angle formed by the ladder and the ground is 68°, how far from the base of the house did he place the ladder?

1 Answer
Dan Kemp
May 21, 2017

Jake would've had to place his #12# foot ladder approximately #4.4952"ft"# from the base of the house to form an angle of #68^@#between the ladder and the ground.

Explanation:

To solve this question, we can use some simple trigonometry functions.

in this situation, we can form a triangular diagram to demonstrate how we will do this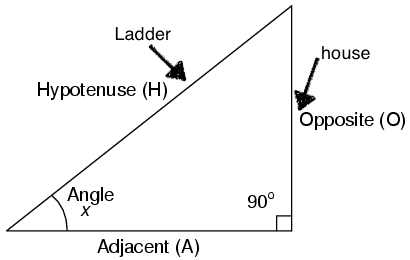enter image source here

As seen here, we will make the Hypotenuse of the triangle as the ladder and the opposite leg to the angle the house. We will try to find the length of the adjacent leg.

#cosx^@ = "Adjacent"/"Hypotenuse"#

#cos68^@ = "Adjacent"/"Hypotenuse"#

#cos68^@ = 0.3746#

#cos68^@ = 1873/5000#

#1873/5000 = x/12#

#1873/5000 = 4.4952/12#

#color(blue)("Adjacent" = 4.4952"ft")#

Related questions
Impact of this question
8457 views around the world
You can reuse this answer
Creative Commons License