Keeping in ming Arrhenius theory, write balanced chemical equations for: a) Aqueous hydrobromic acid and potassium hydroxide b) Aqueous sulphuric acid and barium hydroxide.?
I wrote: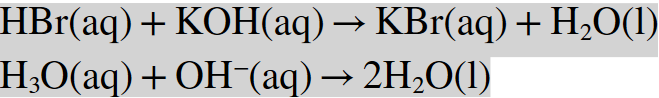
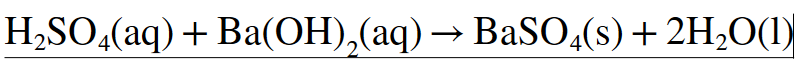
I don't understand the second, also, is first equation correct? Thank you in advance!
I wrote: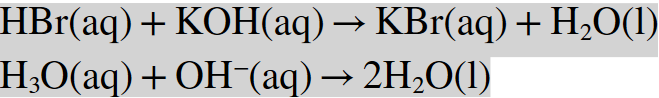
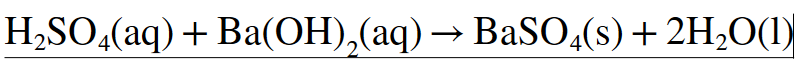
I don't understand the second, also, is first equation correct? Thank you in advance!
1 Answer
Here's what I got.
Explanation:
The Arrhenius Theory of acids and bases categorizes substances that produce hydrogen cations in solution,
For the first reaction, you have hydrobromic acid,
Hydrobromic acid is an Arrhenius acid because it ionizes to produce hydrogen cations in the solution.
#"HBr"_ ((aq)) -> "H"_ ((aq))^(+) + "Br"_ ((aq))^(-)#
Now, you can represent a hydrogen cation as a hydronium cation,
#"HBr"_ ((aq)) + "H"_ 2"O"_ ((l)) -> "H"_ 3"O"_ ((aq))^(+) + "Br"_ ((aq))^(-)#
Potassium hydroxide is an Arrhenius base because it produces hydroxide anions in the solution.
#"KOH"_ ((aq)) -> "K"_ ((aq))^(+) + "OH"_ ((aq))^(-)#
When you mix these two solutions, a neutralization reaction occurs. You can have
# "H"_ ((aq))^(+) + "Br"_ ((aq))^(-) + "K"_ ((aq))^(+) + "OH"_ ((aq))^(-) -> "H"_ 2"O"_ ((l)) + "K"_ ((aq))^(+) + "Br"_ ((aq))^(-)#
Since potassium bromide, one of the products of the reaction alongside water, is soluble in water, you can eliminate the spectator ions
#"H"_ ((aq))^(+) + color(red)(cancel(color(black)("Br"_ ((aq))^(-)))) + color(red)(cancel(color(black)("K"_ ((aq))^(+)))) + "OH"_ ((aq))^(-) -> "H"_ 2"O"_ ((l)) + color(red)(cancel(color(black)("K"_ ((aq))^(+)))) + color(red)(cancel(color(black)("Br"_ ((aq))^(-))))#
to get the net ionic equation.
#"H"_ ((aq))^(+) + "OH"_ ((aq))^(-) -> "H"_ 2"O"_ ((l))#
If you replace the hydrogen cations with the hydronium cations, you get
#"H"_ 3"O"_ ((aq))^(+) + "OH"_ ((aq))^(-) -> 2"H"_ 2"O"_ ((l))#
The same logic applies to the reaction between sulfuric acid and barium hydroxide. This reaction involves an Arrhenius acid that produces
This time, you get
#"H"_ 2"SO"_ (4(aq)) + "Ba"("OH")_ (2(aq)) -> "BaSO"_ (4(aq)) + 2"H"_ 2"O"_ ((l))#
because you have
#"H"_ 2"SO"_ (4(aq)) -> 2"H"_ ((aq))^(+) + "SO"_ (4(aq))^(2-)#
#"Ba"("OH")_ (2(aq)) -> "Ba"_ ((aq))^(2+) + 2"OH"_ ((aq))^(-)#
So when you mix these two solutions, the barium cations and the sulfate anions act as spectator ions
#2"H"_ ((aq))^(+) + color(red)(cancel(color(black)("SO"_ (4(aq))^(2-)))) + color(red)(cancel(color(black)("Ba"_ ((aq))^(2+)))) + 2"OH"_ ((aq))^(-) -> color(red)(cancel(color(black)("Ba"_ ((aq))^(2+)))) + color(red)(cancel(color(black)("SO"_ (4(aq))^(2-)))) + 2"H"_ 2"O"_ ((l))#
which means that you have
#2"H"_ ((aq))^(+) + 2"OH"_ ((aq))^(-) -> 2"H"_ 2"O"_ ((l))#
which can be simplified to
#"H"_ ((aq))^(+) + "OH"_ ((aq))^(-) -> "H"_ 2"O"_ ((l))#

