Kindly answer this question?
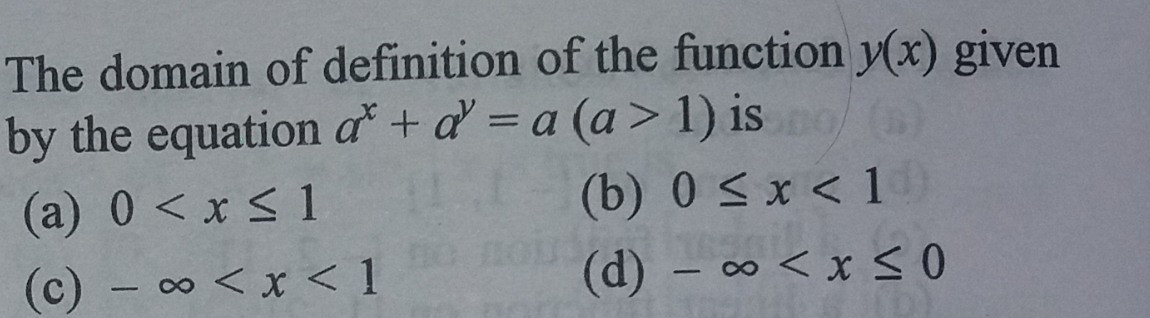
1 Answer
Apr 7, 2017
Explanation:
Solve the function for
Since the logarithm can only accept values greater than
Since
Thus, the domain is
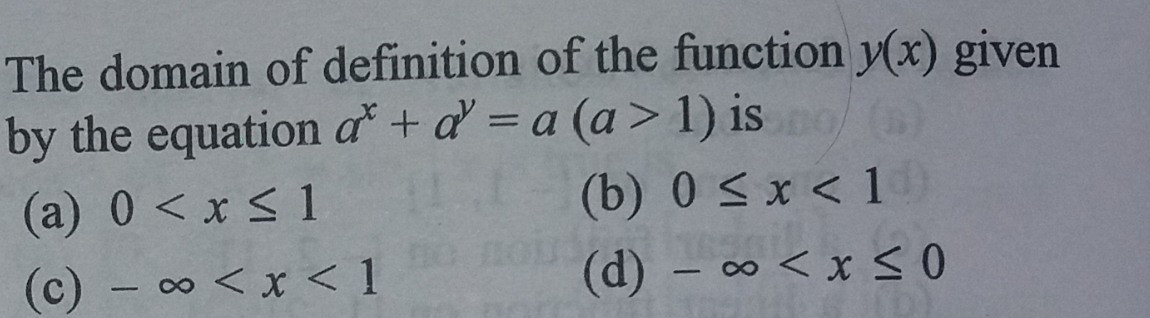
Solve the function for
Since the logarithm can only accept values greater than
Since
Thus, the domain is