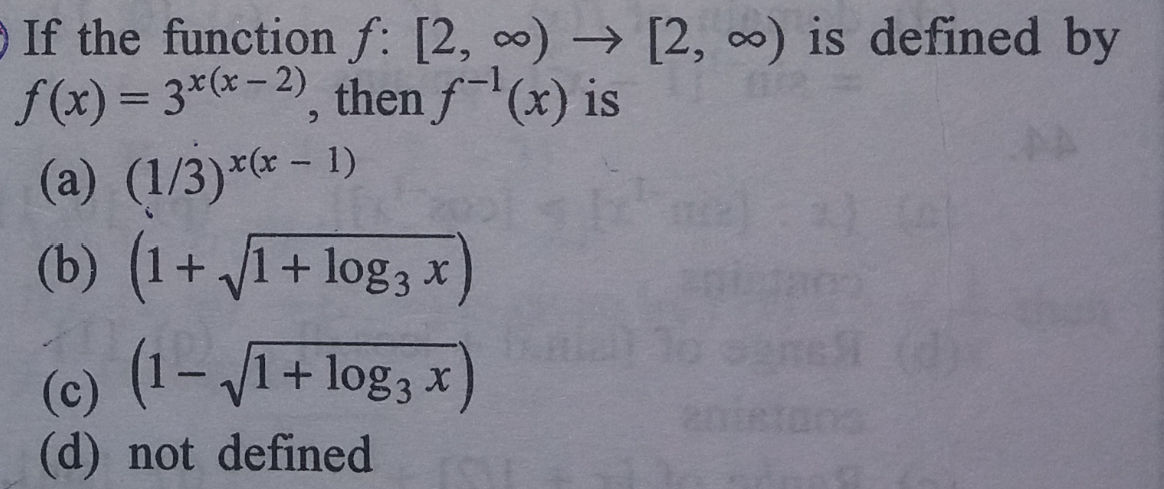graph{y=(3^(x(x-2)))sqrt(x-2)/sqrt(x-2) [-1, 20, -1, 10]}
Graph of #y=3^(x(x-2))# with #x≥2#*
First, we need to be sure that #f# does have an inverse. Looking at the graph above, we see that it should have an inverse function by the horizontal line test.
To solve for its inverse function, we need to solve for #x# in terms of #y# in #y=3^(x(x-2))# and switch #x# and #y#.
Take the logarithm with base #3# on both sides: #log_3(y)=x(x-2)#.
This can be written as a quadratic equation and solved by completing the square. Since #x^2-2x=log_3(y)#, #x^2-2x+1=log_3(y)+1#.
The right-hand side is basically #(x-1)^2#. Now, we take the square root of both sides (remembering the #+-# sign) to get #x-1=+-sqrt(log_3(y)+1)#. Solving for #x#, we get #x=1+-sqrt(log_3(y)+1)#.
However, in the original function, both #x# and #y# is defined as greater than or equal to #2#. The only solution is #x=1+sqrt(log_3(y)+1)# since #1-sqrt(log_3(y)+1)<2# for all #y≥2#.
Finally, after swapping #x# and #y#, we obtain the inverse function #f^-1(x)=1+sqrt(log_3(x)+1)#.