Kindly solve this? which option is correct?
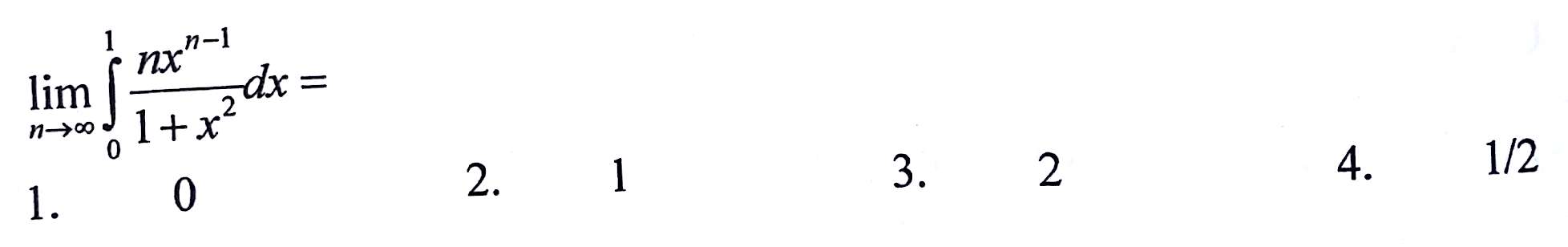
3 Answers
This is readily seen as not doable by elementary means, so I just solved it numerically and got:

I evaluated the integral for
See below.
Explanation:
or
Now assuming that one of the answers is true, the most natural seems to be the fourth 4)
NOTE
for
Explanation:
As has already been shown in a previous solution,
exists and is bounded :
Now integration by parts yields
Now , since
Since
Hence



