Kindly solve this using coordinate geometry?
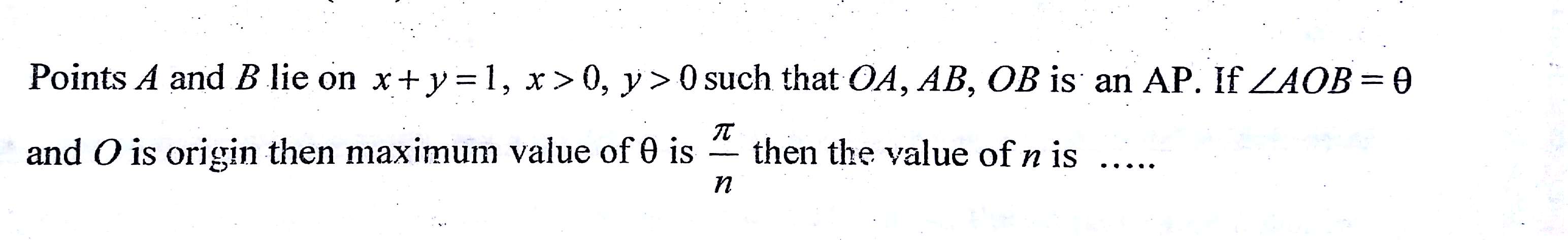
1 Answer
Jan 31, 2018
Explanation:
We know that
and also
and after substitution
Now making
then, the value of
Concluding,
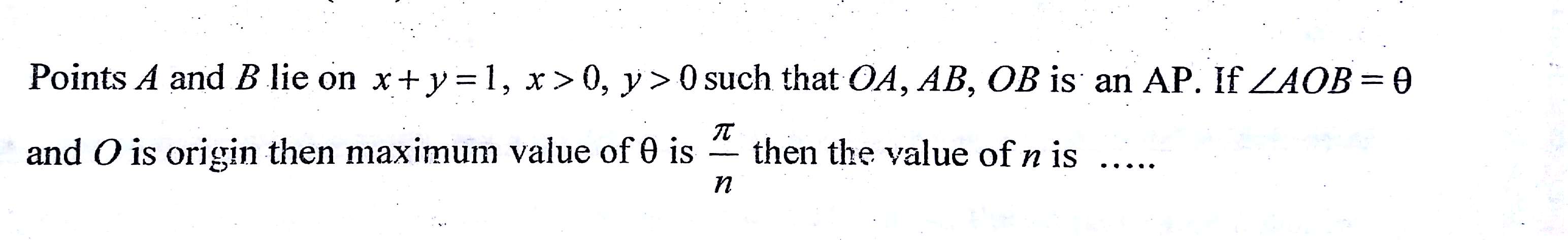
We know that
and also
and after substitution
Now making
then, the value of
Concluding,