L'Hospital's Rule question: Find #\lim_{t\rightarrow\infty}v(t)#?

Question

The downward velocity #v# of a skydiver with nonlinear air resistance can be modeled by:
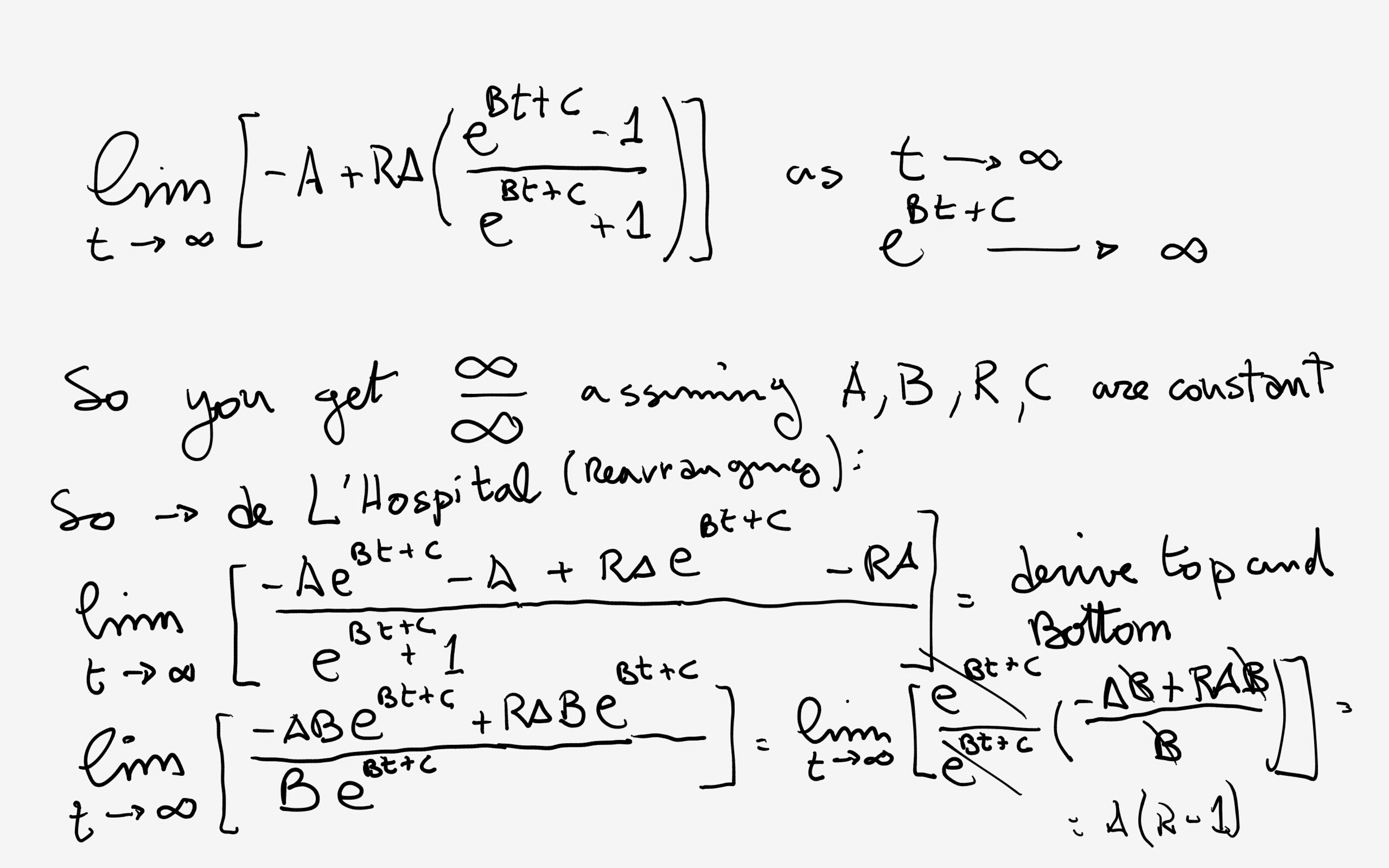
#v=v(t)=-A+RA((e^(Bt+C)-1)/(e^(Bt+C)+1))#

Note

please apply the rule if necessary, as it is in this section.

this is Calculus I/Single Variable
any further advanced explanations can be added if you want...

2330 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-26T12:31:42

I found #A(R-1)# but check my maths because I did it in a hurry and I may have overlooked something...

Have a look:
enter image source here

Answer 2 · 2016-11-26T12:41:00

Depends on #B# sign:
#B > 0->v(oo)=A(R-1)#
#B < 0->v(oo)=A(R(e^C-1)/(e^C+1)-1)#

Supposing #B > 0#

#(e^(Bt+C)-1)/(e^(Bt+C)+1)=e^(Bt)/e^(Bt)((e^C-e^(-Bt))/(e^C+e^(-Bt)))=(e^C-e^(-Bt))/(e^C+e^(-Bt))#

Now #lim_(t->oo)e^(-Bt)=0# so

#v(oo)=lim_(t->oo)(-A+RA((e^C-e^(-Bt))/(e^C+e^(-Bt))))=A(R-1)#

Supposing #B < 0#

#lim_(t->oo)e^(Bt)=0# so

#v(oo)=A(R(e^C-1)/(e^C+1)-1)#

l'Hopital's rule is not needed because the limit is well defined.