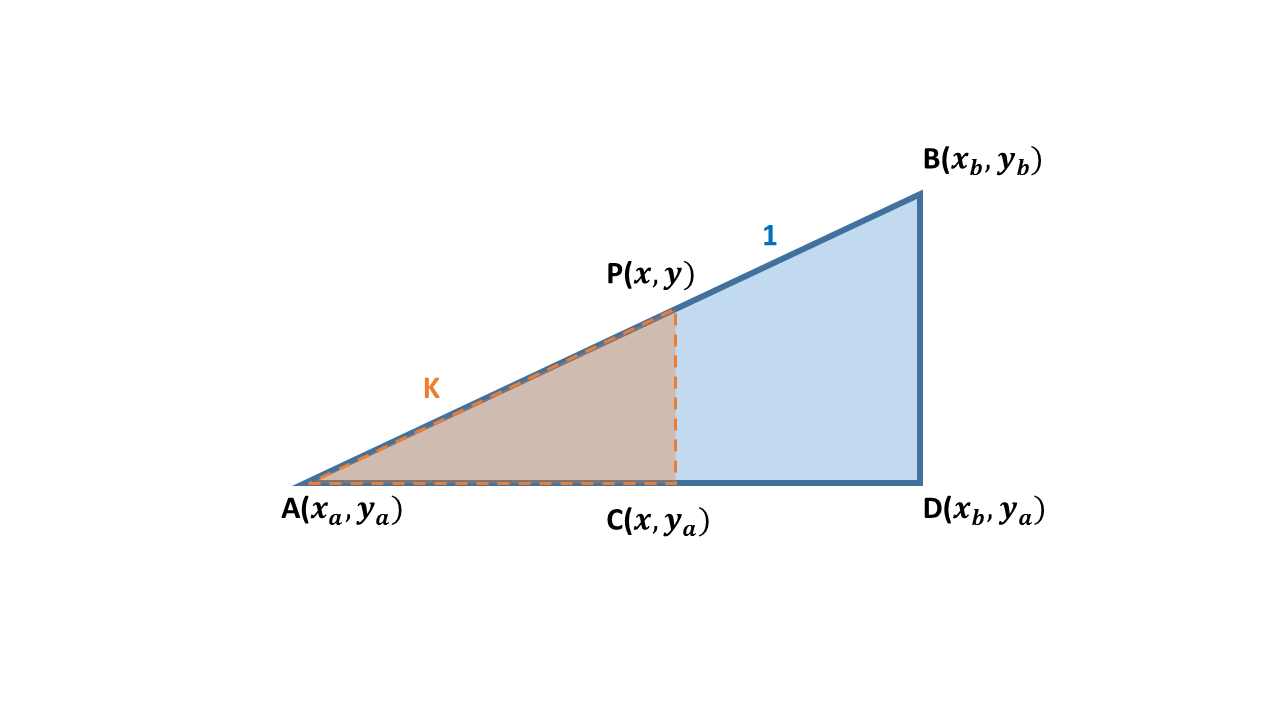
Let #A(x_a,y_a)# and #B(x_b,y_b)# be two points in the plane and let #P(x,y)# be the point that divides #bar(AB)# in the ratio #k :1#, where #k>0#. Show that #x= (x_a+kx_b)/ (1+k)# and #y= (y_a+ky_b)/( 1+k)#?

Question

1623 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-18T17:15:17

See proof below

Let's start by calculating #vec(AB)# and #vec(AP)#

We start with the #x#

#vec(AB)/vec(AP)=(k+1)/k#

#(x_b-x_a)/(x-x_a)=(k+1)/k#

Multiplying and rearranging

#(x_b-x_a)(k)=(x-x_a)(k+1)#

Solving for #x#

#(k+1)x=kx_b-kx_a+kx_a+x_a#

#(k+1)x=x_a+kx_b#

#x=(x_a+kx_b)/(k+1)#

Similarly, with the #y#

#(y_b-y_a)/(y-y_a)=(k+1)/k#

#ky_b-ky_a=y(k+1)-(k+1)y_a#

#(k+1)y=ky_b-ky_a+ky_a+y_a#

#y=(y_a+ky_b)/(k+1)#