Let f=(x/2)+3 be defined on the closed interval {-2,4}, estimate the area under the graph of f above the x-axis using: a. 6 left endpoint rectangles b) 6 right endpoint rectangles?

1 Answer
Geoff K.
May 21, 2018

Left endpoint rectangles: #19.5#.
Right endpoint rectangles: #22.5#.

Explanation:

Estimating the area under a graph is a preview of integration. In integration, we're interested in finding the exact area under a graph between two endpoints.

Here is the exact area we are trying to estimate:

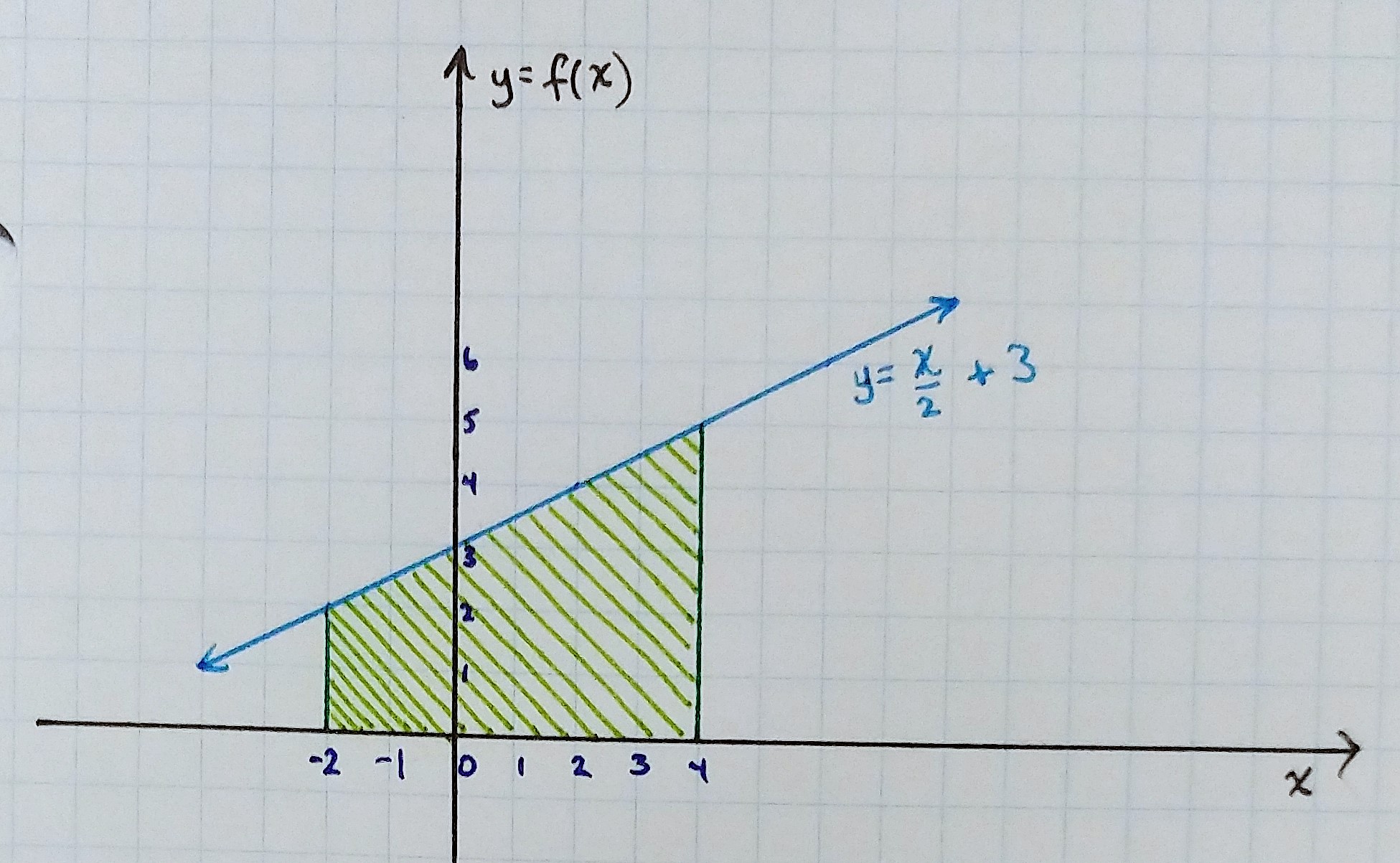
The interval #[–2, 4]# is 6 units wide, and so it is easy enough to divide it into 6 smaller intervals, each 1 unit wide. These will be the widths of our rectangles. But what should we use for the heights?

a) Left endpoint rectangles

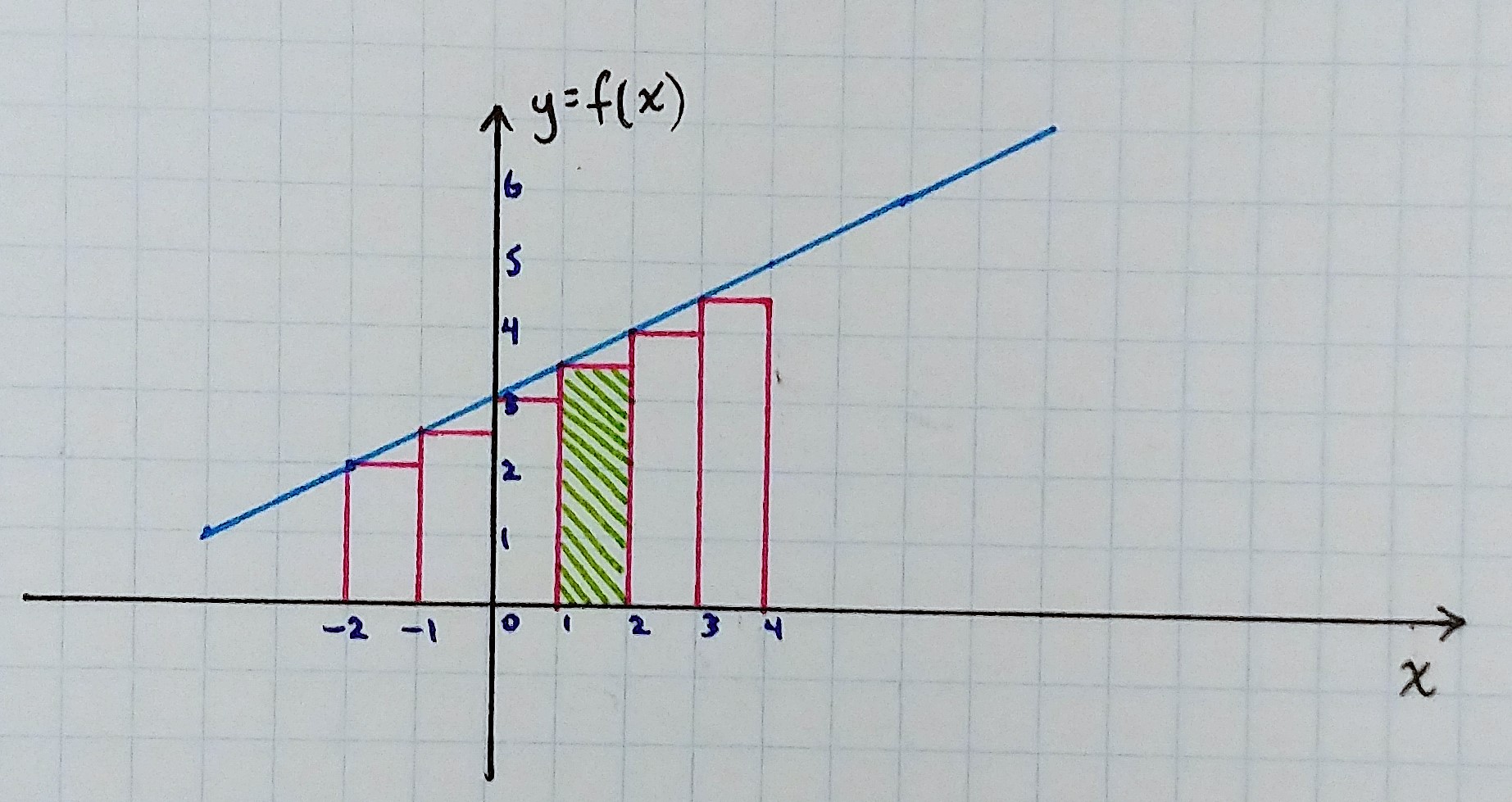
One way is to choose the heights to be the function value for the left endpoint. For example, between #x=1# and #x=2#, our width is #2-1=1# and our height is #f(1)#. See the picture below:

In general, for each interval #[x," " x+1],# the width of the rectangle is #(x+1) - x = 1,# and the height is #f(x)#.

Using this method, our estimate of the function area is

#sum_(x=–2)^3color(gray)(stackrel"rectangle width"overbracecolor(black)[[(x+1) - x]])*color(gray)(stackrel"height"overbrace color(black)f(x))#

# = sum_(x=–2)^3f(x)#

# = f(–2)+f(–1) + f(0) + f(1) + f(2) + f(3)#

#=2 + 2.5 + 3 + 3.5 + 4 + 4.5#

#= 19.5#

b) Right endpoint rectangles

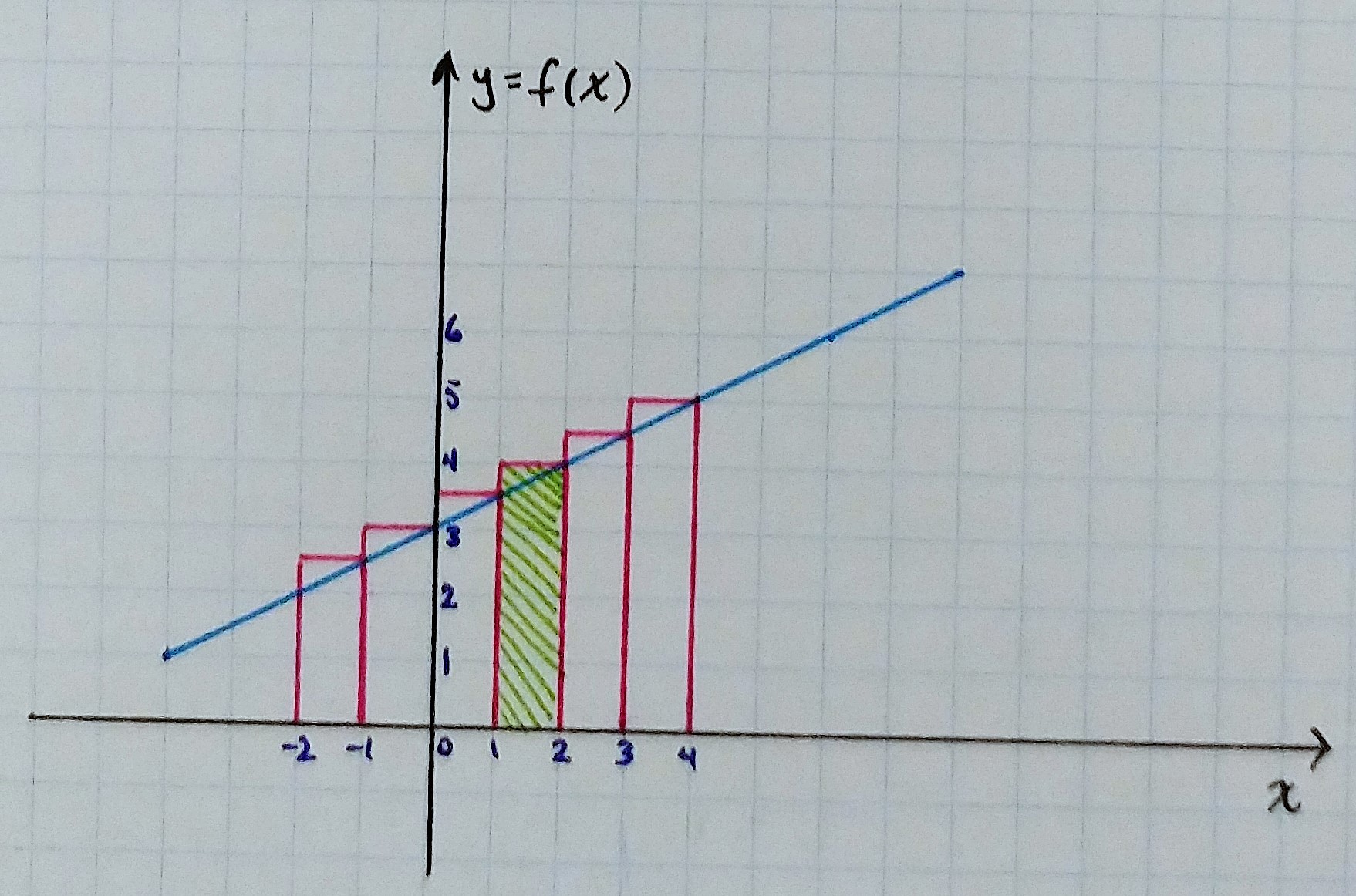
Another way is to choose the heights to be the function value at the right endpoint. For example, between #x=1# and #x=2#, our width is #2-1=1# and our height is #f(2)#. See the picture below:

In general, for each interval #[x," " x+1],# the width of the rectangle is #(x+1) - x = 1,# and the height is #f(x+1)#.

Using this method, our estimate of the function area is

#sum_(x=–2)^3color(gray)(stackrel"rectangle width"overbracecolor(black)[[(x+1) - x]])*color(gray)(stackrel"height"overbrace color(black)f(x+1))#

# = sum_(x=–2)^3f(x+1)#

With some summation magic, this becomes

# = sum_(x=–1)^4f(x)#

# = f(–1) + f(0) + f(1) + f(2) + f(3) + f(4)#

#=2.5 + 3 + 3.5 + 4 + 4.5 + 5#

#= 22.5#

Bonus:

Since our shape is a trapezoid, the actual area under the graph of #f(x)# between –2 and 4 is

#A=(b_1+b_2)/2 * h#

#color(white)A = (2 + 5)/2 *[4-(–2)]#

#color(white)A = 7/2 * 6#

#color(white)A = 21#

This is exactly halfway between our two calculated estimates. Can you see why?

Related questions
Impact of this question
1318 views around the world
You can reuse this answer
Creative Commons License