Question

Let g(x)=`int_0^xf(t)dt` where `f` is the function whose graph is shown. Evaluate g(0), g(2), g(4), g(6) and g(12)?

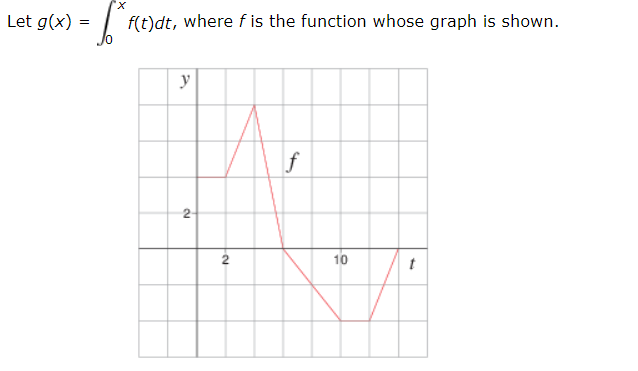
I find that g(0)=0. I think that g(2) should be 4 since the area is 4 squares but its not correct?

Answer 1

`g(0) = 0`
`g(2) = 8`
`g(4) = 20`
`g(6) = 28`
`g(12) = 8`

Explanation:

We have:

`g(x) =int_0^x \ f(t) \ dt`

So that `g(x)` provides the (net) area under the curve from the origin to `x`.

Part (1):

`g(0) = int_0^0 \ f(t) \ dt`
`\ \ \ \ \ \ \= 0 \ \ \` (By definition)

Part (2):

`g(2) = int_0^2 \ f(t) \ dt`
`\ \ \ \ \ \ \= 4 xx 2 \ \ \` (Area of rectangle)
`\ \ \ \ \ \ \= 8`

Part (3):

`g(4) = int_0^4 \ f(t) \ dt`
`\ \ \ \ \ \ \= g(2) + 1/2(4+8)(2) \ \ \` ( + trapezium)
`\ \ \ \ \ \ \= 8 +12`
`\ \ \ \ \ \ \= 20`

Part (4):

`g(6) = int_0^6 \ f(t) \ dt`
`\ \ \ \ \ \ \= g(4) + 1/2(2)(8) \ \ \` ( + `triangle`)
`\ \ \ \ \ \ \= 20+8`
`\ \ \ \ \ \ \= 28`

Part (5):

`g(12) = int_0^12 \ f(t) \ dt`
`\ \ \ \ \ \ \= g(6) - 1/2(8+2)(4) \ \ \` ( + trapezium below)
`\ \ \ \ \ \ \= 28 - (10(2)`
`\ \ \ \ \ \ \= 8`