Let R be the region bounded by #y = 1/x#, #y = x^2#, #x = 0#, and #y = 2# and revolved about the x axis. How do you find the volume of rotation using: a) the method of cylindrical shells; b) the method of circular disks?
1 Answer
Explanation:
Because we are looking at revolution about an horizontal axis, using cross-section (See videos 1 through 6 here if you need a refresher) is more natural, so let us start with that.
Here is the region we are rotating about the
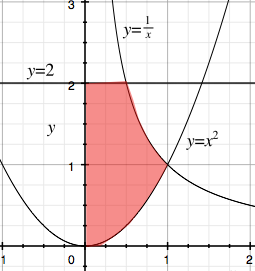 .
.
The first thing to understand is where the curves intersect.
So the expression for the area
Namely, for
On the other hand if
As a result, the volume of the resulting solid of revolution is
On other hand,
Hence, altogether, we obtain
Considering the length of the answer, I am leaving the cylindrical shell part to another time.


