Question

Let there be spherically symmetric charge distribution with charge density P(x)=Pₒ[(5/4)-(r/R)] up-to r=R, P(r)=0 for r≻R. Where 'r'is the distance from origin. What is the electric field at a distance 'r' (r≻R) form the origin?

Answer 1

`=rho_o/(4epsilon_o)(5/3-r/R)`

Explanation:

volume charge density, `rho(r)=rho_o(5/4-r/R),` upto `r=R`
`=>(dq)/(dV)=rho_o(5/4-r/R)`
`=>dq=rho_o(5/4-r/R)dV...(i)`

consider a sphere of radius R

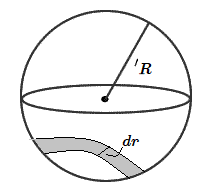
let a thin strip of radius `dr`
the surface area of the strip is `4pir^2` and thickness is `dr`
so, the small volume of the strip is `dV=4pir^2dr`
now
substitute for `dV` in `(i)`
`dq=rho_o(5/4-r/R)4pir^2dr`

now integrate to find out total charge enclosed till any point 'r'
`=>q=intrho_o(5/4-r/R)4pir^2dr`
`=>q=rho_opir^3(5/3+r/R)`
now electric field at ny point at a distance r is given by
`E=kq/r^2=(krho_opir^3(5/3-r/R))/r^2`
`=rho_o/(4epsilon_o)(5/3-r/R)`

Answer 2

`E(r) = ( rho_o R^3)/(6 \ varepsilon_o ) * 1/r^2`

Explanation:

• `rho(r) = {( rhoₒ(5/4-r/R), 0 le r le R),(0, r gt R):}`

Gauss' Law states that:

• The total of the electric flux `Phi` out of a closed surface is equal to the total charge enclosed divided by the permittivity:

• `Phi = Q_("enc")/varepsilon_o`

If we draw a Gaussian sphere enclosing, and with the same origin as, this spherically symmetric charge distribution, then:

• The total of the electric flux out of the Gaussian sphere is equal to E-field at the surface times the surface's area:

• `Phi = E(r) * 4 pi r^2`.

IOW, for a Gaussian sphere , concentric with the charge distribution, and of radius `r gt R`:

• `E(r) = Q_("enc")/(4 pi varepsilon_o r^2)` (Coulomb's Law with the distribution treated as a point charge)

(1) Find `Q_("enc")`

`Q_("enc") = int_V rho(r) \ dV`

For a sphere:

• `V = 4/3 pi r^3, qquad dV = 4 pi r^2 dr`

`Q_("enc") = 4 pi rho_o int_0^R (5/4-r/R) r^2 \ dr`

`= 2/3 pi rho_o R^3`

(2) Find `E(r), qquad r gt R`

`E(r) = Q_("enc")/(4 pi varepsilon_o r^2)`

`= ( rho_o R^3)/(6 \ varepsilon_o ) * 1/r^2`