Question

Let XY be the diameter of a semicircle with centre O.let A and B variable points on the semicircle such that AB is parallel to XY.then, give value of angle BOY for which the inradius of triangle AOB is maximum??also show steps of solution, please.thanks.

Answer 1

`angleBOY=x=0.90455` rad

Explanation:

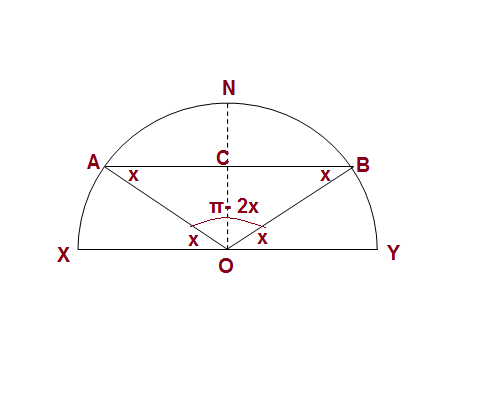
Given
Let XY be the diameter of a semicircle with centre O.let A and B variable points on the semicircle such that AB is parallel to XY.

Let the `angleBOY=x` rad.

We are to find out the value of angle BOY for which the in radius of triangle AOB is maximum.

`ON` is drawn perpendicular to both `XY and AB`

Let the radius of the semi circle be `R` and radius of the in radius of the `Delta AOB` is `r`. So `AO=OB=R and angle AOB=pi-2x`

Now area of the `DeltaAOB=1/2*OA*OB*sin(pi-2x)`

`=>DeltaAOB=1/2*R*R*sin(2x)=R^2sinxcosx`

Now `AC=BC=Rcosx=>AB=2Rcosx`

So semi perimeter of `DeltaAOB`

`s=1/2(OA+OB+AB)=1/2(R+R+2Rcosx)`

Hence `s=R(1+cosx)`

Applying relation between area of the `Delta AOB` with its in radius `r`.

`r=(DeltaAOB)/s=(R^2sinxcosx)/(R(1+cosx))`

`=>r=(Rsin(x)cos(x))/(1+cos(x))`

`=>r=R*f(x)`,where `f(x)=(sin(x)cos(x))/(1+cos(x))`

In this relation `R` is a constant and `x in (0.pi/2)`

So `r_"max"=R*f_"max"(x)`

Now

`f(x)=(sin(x)cos(x))/(1+cos(x))`

`=>f(x)=(2sin(x/2)cos(x/2)cos(x))/(2cos^2(x/2))`

`=>f(x)=tan(x/2)cos(x/2)`

For maximum value of `x`, `f'(x)=0`

Hence

`1/2sec^2(x/2)cos(x)-tan(x/2)sinx=0`

`=>(1+tan^2(x/2))/(2tan(x/2))cos(x)=sinx`

`=>cos(x)/sin(x)=sin(x)`

`=>cos(x)=sin^2(x)`

`=>cos^2(x)+cos(x)-1=0`

`=>cos(x)=(-1+sqrt(1^2-4*1*(-1)))/2`

`=>x=cos^-1((sqrt5-1)/2)~~0.90455` rad

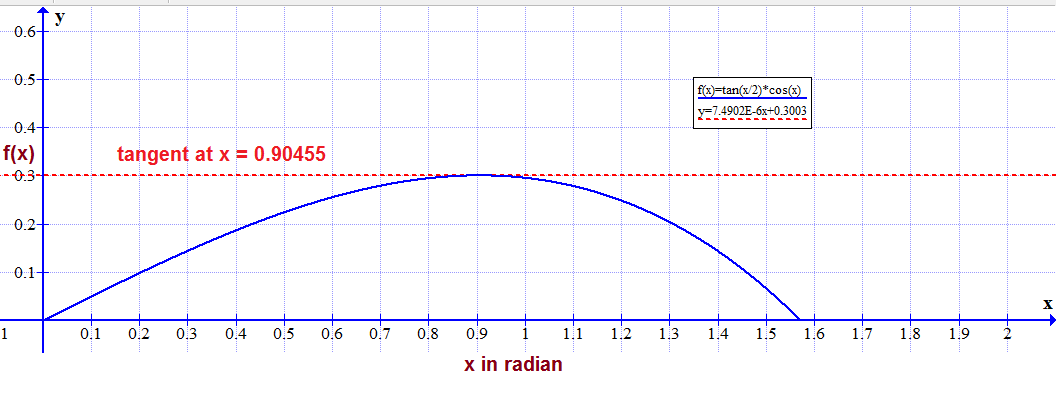
The following `f(x)" vs " x` plot supports the above result.