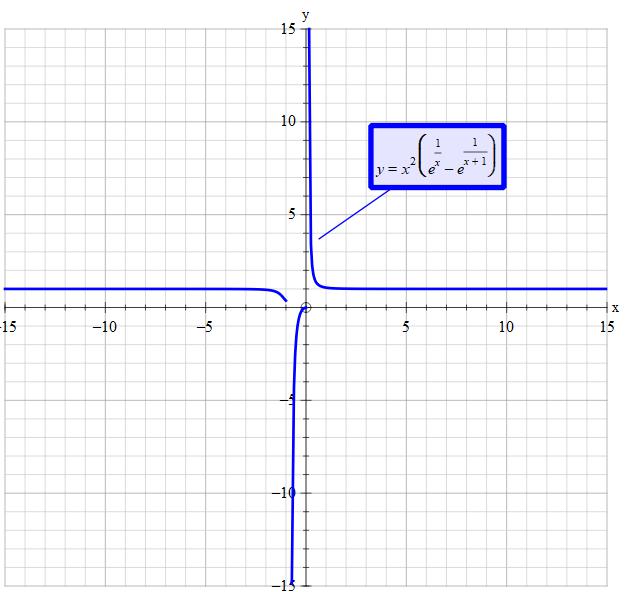
lim_(x->+oo) (x)^2 (e^(1/(x))-e^(1/(x+1))) ?
lim_(x->+oo) color(white)(..)(x)^2 (e^(1/(x))-e^(1/(x+1))) ?
1 Answer
Explanation:
Here's a slightly quick and dirty method using the series for
Note that:
e^t = 1+t+t^2/2+t^3/6+...
So:
e^(1/x)-e^(1/(x+1)) = (1+1/x+1/(2x^2)+...)-(1+1/(x+1)+1/(2(x+1)^2)+...)
color(white)(e^(1/x)-e^(1/(x+1))) = 1/(x(x+1))+1/(O(x^3))
So:
lim_(x->oo) x^2(e^(1/x)-e^(1/(x+1))) = lim_(x->oo) (x^2/(x(x+1))+1/(O(x))) = 1
 Tony B
Tony B


