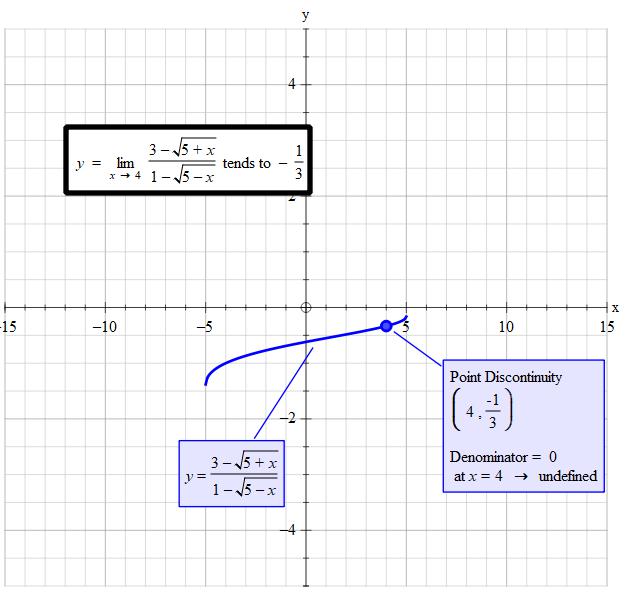
#lim_(x rarr 4) (3 - sqrt(5 + x))/(1- sqrt(5 - x)) = ?#
2 Answers
The limit is
Explanation:
It is similar to both
but both in one expression.
So multiply
# = lim_(xrarr4)((4-x)(1+sqrt(5-x)))/((3+sqrt(5+x))(-(4-x))#
# = lim_(xrarr4)(-(1+sqrt(5-x)))/(3+sqrt(5+x))#
# = (-(1+sqrt1))/(3+sqrt9) = -2/6 = -1/3#
The limit should approach -1/3, I screwed up the original answer.
Explanation:
first multiply the top and bottom by the conjugate of the numerator and the conjugate of the denominator
plug in the limit value to get your answer: