Linear Programming: What acreage allows to farmer to maximize profit?
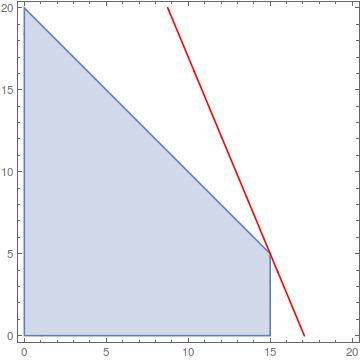
A farmer has a choice of planting a combination of two different crops on 20 acres of land. For crop A, seed costs $120 per acre, and for crop B, seed costs $200 per acre. Government restrictions limit acreage of crop A to 15 acres but do not limit crop B. Crop A will take 15 hours of labor per acre at a cost of $5.60 per hour, and crop B will require 10 hours of labor per acre at $5.00 per hour. The expected income from crop A is $600 per acre, and crop B is $250 per acre. How many acres of each crop should the farmer plant in order to get maximum profit?
I know the answer is 15 acres of A and 5 acres of B, but I don't know how to get there...
Thanks!
A farmer has a choice of planting a combination of two different crops on 20 acres of land. For crop A, seed costs $120 per acre, and for crop B, seed costs $200 per acre. Government restrictions limit acreage of crop A to 15 acres but do not limit crop B. Crop A will take 15 hours of labor per acre at a cost of $5.60 per hour, and crop B will require 10 hours of labor per acre at $5.00 per hour. The expected income from crop A is $600 per acre, and crop B is $250 per acre. How many acres of each crop should the farmer plant in order to get maximum profit?
I know the answer is 15 acres of A and 5 acres of B, but I don't know how to get there...
Thanks!
1 Answer
See below.
Explanation:
Ignoring the costs and considering only the profits you can equate
subjected to
where
giving as optimum result
Attached a plot