Looking for answers for a)iv), a)v) and c)... Is my brain not working or are the answers in my book wrong? An explained answer is much appreciated!
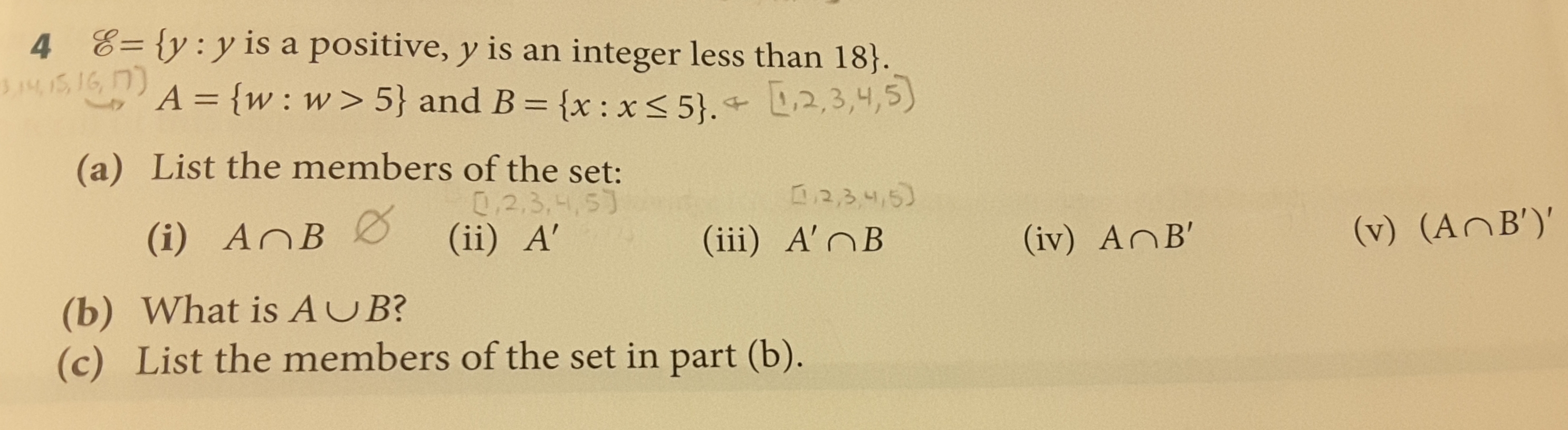

1 Answer
Answers in your book are inconsistent in their definition of set B! The definition for some answers is
and for other answers it is
Explanation:
y is in the set of integers between 1 and 17, inclusive (0 is not considered positive and y is strictly less than 18).
A is the subset of
B is the subset of
OR...
B is the subset of
4 (a) (i) The insection of A and B (the elements that they have in common) is empty.
4 (a) (ii) The subset "Not A" contains all of the elements in
4 (a) (iii) The intersection of "Not A" and B contains all of the elements that these subsets have in common.
4 (a) (iv) The intersection of A and "Not B" contains all of the elements that these subsets have in common.
4 (a) (v) The complement of the intersection of A and "Not B" contains all of the elements EXCEPT those that these subsets have in common.
4 (b) The union of A and B combines the contents of the two subsets, which equals the contents of
4 (c) The book's answer makes NO sense!

