Question

Magnetic Forces between Four parallel copper wires?

Answer 1

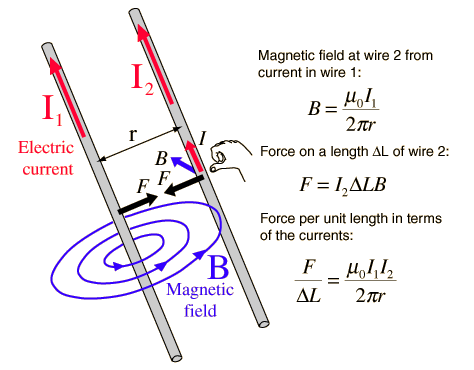
Referring to the figure above and force per unit length between two infinite parallel current carrying wires is given as

`F/(DeltaL)=(mu_0I_1I_2)/(2pir)`

We also know that if currents are parallel to each other these attract and repel if currents are anti-parallel.

In the given question currents are parallel. Each current carrying wire experiences three attractive forces. Two forces are directed along the sides of the square and third force is directed along the diagonal. Total force is resultant of three vectors.

Force per unit length along the side `=(mu_0i^2)/(2pia)`
Force per unit length along the diagonal `=(mu_0i^2)/(2pisqrt2a)`
Now resultant vector of two forces per unit length along the sides `=sqrt(F_1^2+F_2^2)` along the diagonal.
Since moduli of `F_1 and F_2` are equal `:.sqrt(F_1^2+F_2^2)=sqrt2F`
We get sum of all three force per unit length as

`F/(DeltaL)=(sqrt2mu_0i^2)/(2pia)+(mu_0i^2)/(2pisqrt2a)`, directed along the diagonal.
`=>F/(DeltaL)=(mu_0i^2)/(2pia)(sqrt2+1/sqrt2)`

Inserting given values we get

`F/(DeltaL)=(4pixx10^-7xx(18.7)^2)/(2pixx0.245)xx3/sqrt2`
`=>F/(DeltaL)=6.06xx10^-4Nm^-1`, rounded to two decimal places.