Mathematically derive the roots of #color(white)("d")y=x^3-3x-1=0# ?
I have tried Cardano's method but come up with a complex number root. Obviously wrong!
Iterations for the two #x's# yield
#color(white)("d")-1.53208... and -0.34729.. and +1.879.... #
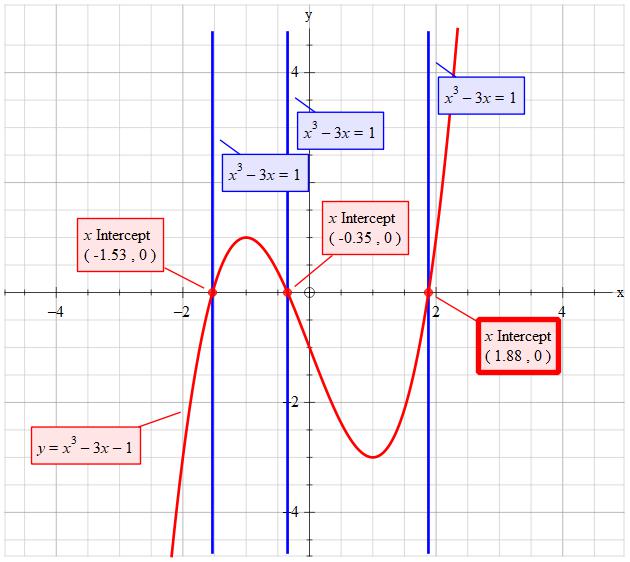
I have tried Cardano's method but come up with a complex number root. Obviously wrong!
Iterations for the two

1 Answer
Explanation:
Given:
#x^3-3x-1 = 0#
Discriminant
The discriminant
#Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd#
In our example,
#Delta = 0+108+0-27+0 = 81#
Since
Trigonometric substitution
Since this cubic has
As an alternative in such cases, I would choose to use a trigonometric substitution.
Let:
#x = k cos theta#
The trick is to choose
We have:
#0 = x^3-3x-1#
#color(white)(0) = k^3 cos^3 theta - 3k cos theta - 1#
#color(white)(0) = k(k^2 cos^3 theta - 3 cos theta) - 1#
#color(white)(0) = 2(4 cos^3 theta - 3 cos theta) - 1" "# with#k=2#
#color(white)(0) = 2cos 3theta - 1#
So:
#cos 3 theta = 1/2#
So:
#3 theta = +-pi/3+2npi" "# for any integer#n#
So:
#theta = +-pi/9+(2npi)/3" "# for any integer#n#
This will give
#x = 2 cos theta = 2 cos(pi/9+(2npi)/3)" "# for#n = 0, 1, 2# .

