Question

Mg was reacted with an excess of HCl dilute and the `H_2` gas produced collected in an eudiometer. The volume of hydrogen in the eudiometer was corrected to conditions of STP. If 94.1 milliliters of H2 was produced, how much Mg reacted in this experiment?

Answer 1

Given `Mg(s) + 2HCl rarr MgCl_2(aq) + H_2(g)uarr`....we gets.....

Explanation:

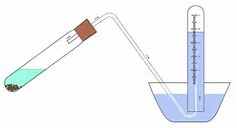
A `"eudiometer"` is a fancy name for a simple setup..as shown in the diagram. Note that as depicted the pressure of gas in the tube is LESS than atmospheric pressure. It is only when level of water inside the column is equal to the level OUTSIDE that the pressures are equal.....i.e. `P_"atmospheric"=P_"gas"+P_"saturated vapour pressure"`. `P_"SVP"="vapour pressure of water"`, a constant at constant temperature.

The stoichiometric equation EXPLICITLY shows stoichiometric equivalence between the metal and dihydrogen.

`"Moles of dihydrogen"=(PV)/(RT)`

`=(0.987*atmxx94.1xx10^-3*L)/(0.0821*L*atm*K^-1*mol^-1xx273.15*K)`

(And if you think all this bumf in converting to LESS than 1 standard atmosphere is a bit tedious, I agree with you!).

`n_(H_2)~=4*mmol`

Given the stoichiometry, we use approx. `4*mmolxx24.3*g*mol^-1=0.1*g` of metal, a good mass for such an experiment.