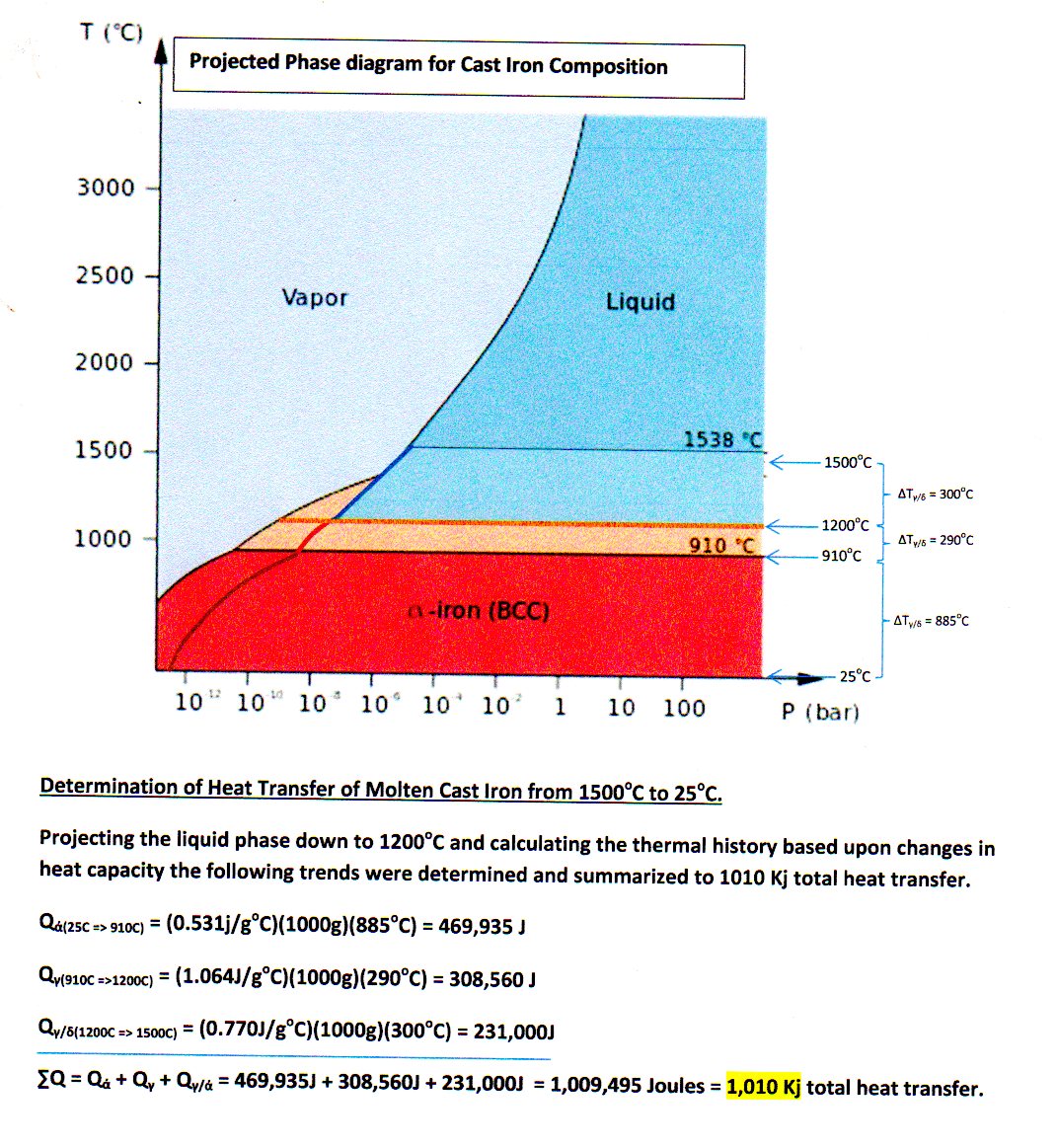
Molten iron is extremely hot, averaging about 1,500 C. The specific heat of iron is 0.46 J/gC. How much heat is released to the atmosphere when 1 kg molten iron cools to room temperature (25 C)?
3 Answers
900 Kj
Explanation:
Since the type of iron is not specified then it is assumed to be 'Cast Iron' which has a melting point of 1204 deg-Celsius*.
*http://www.onlinemetals.com/meltpt.cfm
The total heat transfer would be ,,,
..............................................................................................................................
=>
=
(Specific Heat of Molten Iron) http://www.engineeringtoolbox.com/liquid-metal-boiling-points-specific-heat-d_1893.html
..............................................................................................................................
=>
=
(Heat of Fusion of Molten Iron) http://www.engineeringtoolbox.com/fusion-heat-metals-d_1266.html
...............................................................................................................................
=>
=
(Specific Heat of Iron (s) = 0.46
..............................................................................................................................
I got
You can get more context here:
https://en.wikipedia.org/wiki/Iron#Phase_diagram_and_allotropes
and you can examine the specific heat capacity variations more closely here:
http://webbook.nist.gov/cgi/cbook.cgi?ID=C7439896&Mask=2&Type=JANAFS&Plot=on#JANAFS
On another note, this
If you simply assume a
There is a HUGE assumption here that iron's specific heat capacity doesn't change from
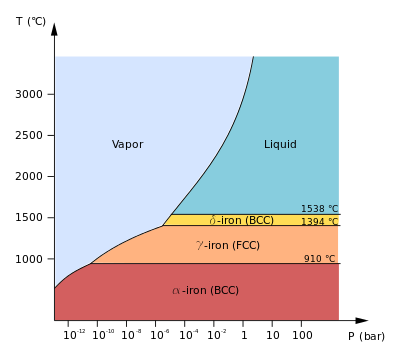
Since all these phases at
However, the specific heat capacity
[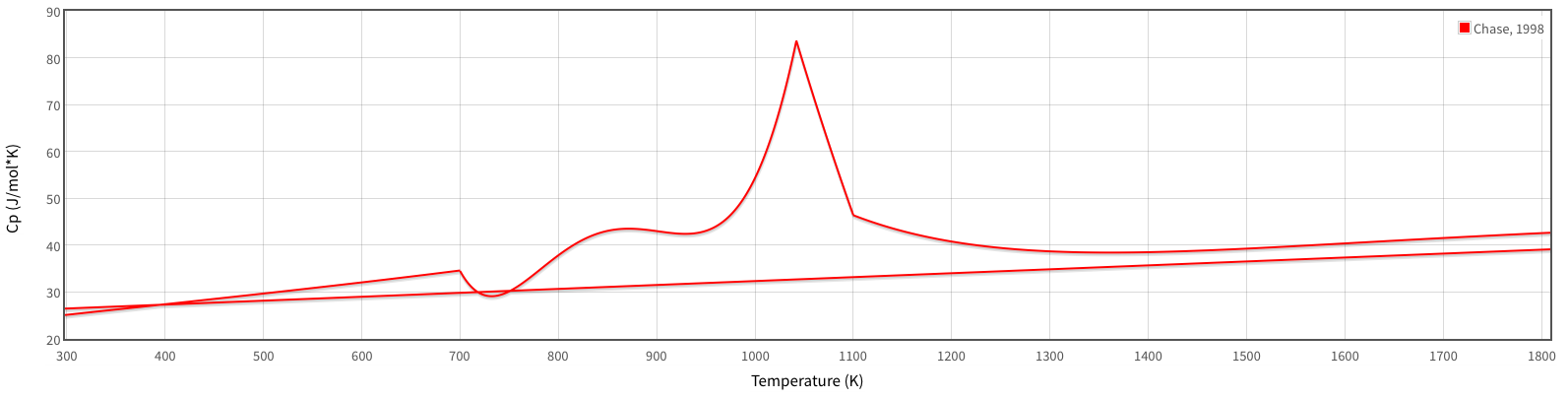
The wonky curve is the
#alpha# -phase, from#"298.15 K"# up to#"700 K"# (#426.85^@ "C"# ), using an average of#C_P ~~ "29.656 J/mol"cdot"K"# (at#~~ "500 K"# ), or#"0.531 J/g"cdot"K"# .#alpha# -phase, from#"700 K"# to#"935 K"# (#661.85^@ "C"# ) using an average of#C_P ~~ "40.149 J/mol"cdot"K"# (at#~~ "816 K"# ), or#"0.719 J/g"cdot"K"# #alpha# -phase, from#"935 K"# to#"1042 K"# (#768.85^@ "C"# ) using an average of#C_P ~~ "59.442 J/mol"cdot"K"# (at#~~ "1010 K"# ), or#"1.064 J/g"cdot"K"# #alpha# -phase, from#"1042 K"# to#"1100 K"# (#826.85^@ "C"# ) using an average of#C_P ~~ "65.743 J/mol"cdot"K"# (at#~~ "1068 K"# ), or#"1.177 J/g"cdot"K"# #alpha# -phase, from#"1100 K"# to#"1183.15 K"# (#910^@ "C"# , the#alpha->gamma# transition temperature) using an average of#C_P ~~ "43.029 J/mol"cdot"K"# (at#~~ "1150 K"# ), or#"0.770 J/g"cdot"K"# #gamma# -phase, from#"1183.15 K"# to#"1667.15 K"# (#1394^@ "C"# , the#gamma->delta# transition temperature) using an average of#C_P ~~ "35.856 J/mol"cdot"K"# (at#~~ "1420 K"# ), or#"0.642 J/g"cdot"K"# #delta# -phase, from#"1667.15 K"# to#"1773.15 K"# (#1500^@ "C"# !), using an average of#C_P ~~ "41.764 J/mol"cdot"K"# (at#~~ "1722 K"# ), or#"0.748 J/g"cdot"K"# .
Aren't you glad we aren't doing phase changes? :-)
So, we would have the heat of cooling as the negative of the heat of heating:
#q_"cool" = -(q_1 + . . . + q_7)#
#= -m(C_(P1)DeltaT_(0->1) + . . . + C_(P7)DeltaT_(6->7))#
I'll leave the units out, but you know that they are
#= -1000 cdot [0.531(700 - 298.15) + 0.719(935 - 700) + 1.064(1042 - 935) + 1.177(1100 - 1042) + 0.770(1183.15 - 1100) + 0.642(1667.15 - 1183.15) + 0.748(1773.15 - 1667.15)]#
Each phase then approximately contributes:
#= overbrace(-"628487 J")^(alpha" phase") + overbrace(-"310728 J")^(gamma" phase") + overbrace(-"79288 J")^(delta" phase")#
#~~# #-1.020 xx 10^(6)# #"J"# ,
or about
Thermal history of cooling cast iron
Explanation:
Thermal history of cooling cast iron from