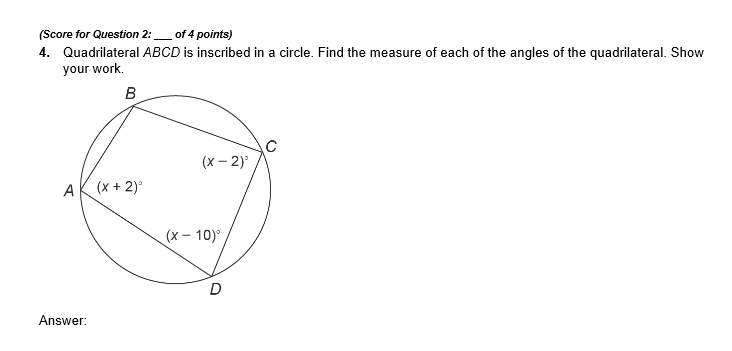
Need help with a geometry question?
2 Answers
Explanation:
Let x equal the angle of
Angle
Angle
Angle
Substitute your x-value into A, C, and D.
Please read the explanation.
Explanation:
Given:
Analyze the problem constructed using a geometry software available below:
Please note that the diagram is not drawn to scale.
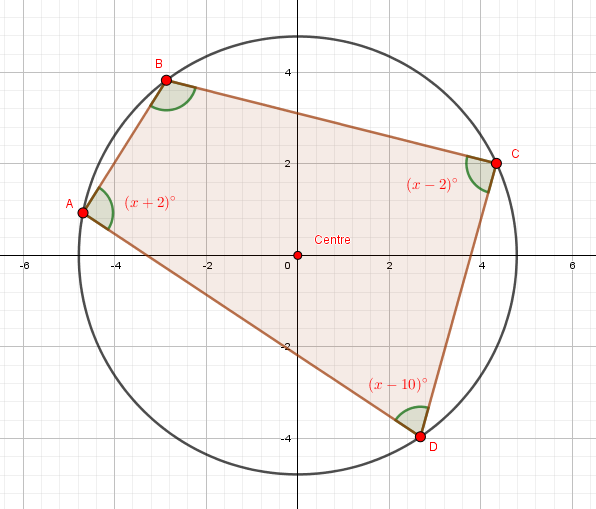
We observe the following:
-
The quadrilateral ABCD is inscribed in a circle.
-
ABCD is a cyclic quadrilateral, since all the vertices of the quadrilateral touch the circumference of the circle.
Properties associated with angles in cyclic quadrilaterals:
The opposite angles of a cyclic quadrilateral add to
We can use this useful property to solve our problem by chasing angles:
Hence,
Given that
As,
As,
Consider Equation 2 first.
Divide both side by 2
Hence,
So, when
We know that
Subtract
Now, we are in a position to write all our angles as follows:
Next, let us verify all the four angles add to


