Objects A and B are at the origin. If object A moves to #(3 ,-2 )# and object B moves to #(2 ,9 )# over #5 s#, what is the relative velocity of object B from the perspective of object A? Assume that all units are denominated in meters.
1 Answer
Oct 10, 2016
Relative velocity of
Explanation:
After moving
from
for a distance of
Since this apparent motion takes place over
the apparent speed is
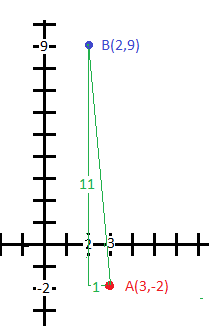
The angle of this apparent motion,
