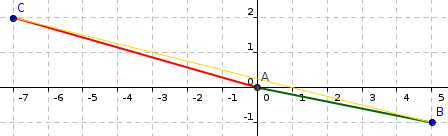
Objects A and B are at the origin. If object A moves to #(5 ,-1 )# and object B moves to #(-7 ,2 )# over #3 s#, what is the relative velocity of object B from the perspective of object A? Assume that all units are denominated in meters.
2 Answers
The question is about velocity which is a vector, hence you need to consider size and direction.
Explanation:
From A's perspective, B will have moved a distance of 12m in the negative x direction (5--7) and 3m in the positive y direction (2--1).
If you are using i and j as unit vectors in the x and y direction, then the displacement vector relative to B would be -12i + 3j. Hence dividing by 3 gives the velocity vector of -4i+ j.
If you are not using this notation, the total distance using Pythagoras = the square root of (12 squared + 3 squared) = 12.4m. Over 3 seconds, this equates to 4.1m/s (an assumption being that points are not accelerating relative to each other).
In terms of direction, you can work this out using trigonometry by defining an angle. This is easier to see if you plot on a graph, but if you defined the positive y axis as 0 degrees, then the angle would be (270 + tan-1 (3/12)
Explanation: