On what interval is the function f (x) = x^3 e^x increasing?
2 Answers
Explanation:
STEP 1: Remember that our function,
STEP 2: Find the zeros of the function.
STEP 3: Use a sign chart to determine when
STEP 3a: Plug any value less than -3 into the
When
STEP 3b: Plug in any value between -3 and 0 into
When
STEP 3c: Plug any value greater than 0 into the
when
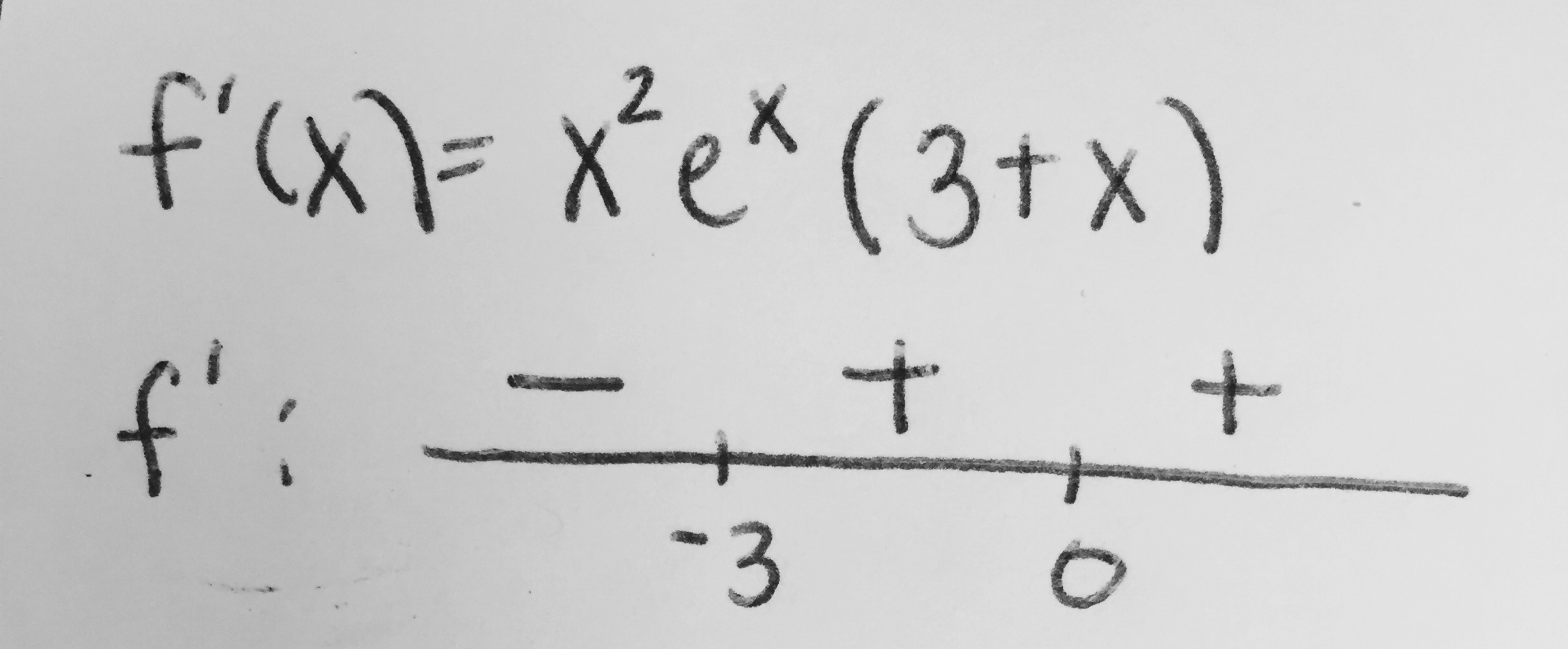
ANSWER:
—Note that
The interval of increasing of
Explanation:
We need
The function is
This is a product of two functions
Therefore,
The critical points are when
Therefore, the critical points are when
We can make a sign chart
The interval of increasing of
graph{x^3e^x [-12.66, 12.65, -6.33, 6.33]}



