One body is thrown vertically upward with initial velocity of 20m/s.2 seconds later another is vertically thrown from the same place with the same speed.at what height will they collide?

2 Answers
Jane
Feb 14, 2018

Suppose,the 1st ball is thrown upwards,it went upto its maximum height(#H#) and started falling down,so in its way it will meet the 2nd ball rising up.

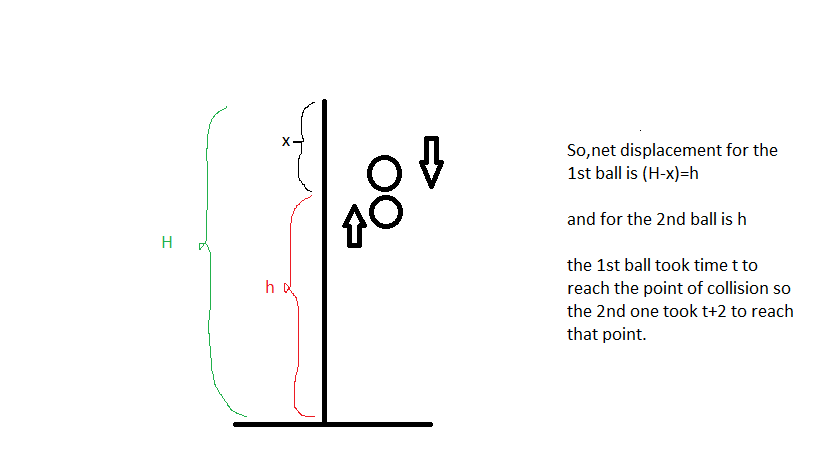
enter image source here

So,in that time,if the 1st ball comes down by #xm#,its net displacement will be #H-x=h#(let)

Now,at that moment,the 2nd ball must also have an upward displacement of #h#,and that's why the collision will occur.

So,we can write, #h= ut - 1/2 g t^2# (for the 1st ball)

And, #h=u(t+2) - 1/2g (t+2)^2# (as the 2nd ball will have the same displacement in time #(t+2)#)

So,equating both we get,

#t= (u-g)/g = (20-10)/10 =1 s#

So, putting in either of the equation,we get the height #h# at which the collision will take place, is #15 m# above the ground.

A08
Apr 5, 2018

Collision will occur if one (first) ball is falling down and second ball is moving up. Let these collide at a height #h# after time #t# when first ball is thrown up.

Kinematic expression which can be used is

#h=ut+1/2g t^2#

For first ball.
Remembering that gravity acts in a direction opposite to initial direction of motion and taking origin of coordinates at the ground level from where balls are thrown up.

#h=20t+1/2(-9.81) t^2# ......(1)

For the second ball

#h=20(t-2)+1/2(-9.81) (t-2)^2# .....(2)

Equating RHSs of both equations we get

#20t+1/2(-9.81) t^2=20(t-2)+1/2(-9.81) (t-2)^2#
#=>0=20(-2)+1/2(-9.81) (-2t+4)#
#=>9.81t=40-19.62#
#=>t=2.077\ s#

From (1) we get

#h=20xx2.077-1/2(9.81) (2.077)^2#
#h=20.38\ m#

Related questions
Impact of this question
8532 views around the world
You can reuse this answer
Creative Commons License