One problem on physics, center of mass?
A man is pushing a cylinder of mass #m_1# with the help of a flat plank of mass #m_2# . The horizontal component of the applied force is #F# . If no touching surface does not slip,then
i)acceleration of plank and center of mass of cylinder...
ii)Value of frictional force in the touching point and its direction.
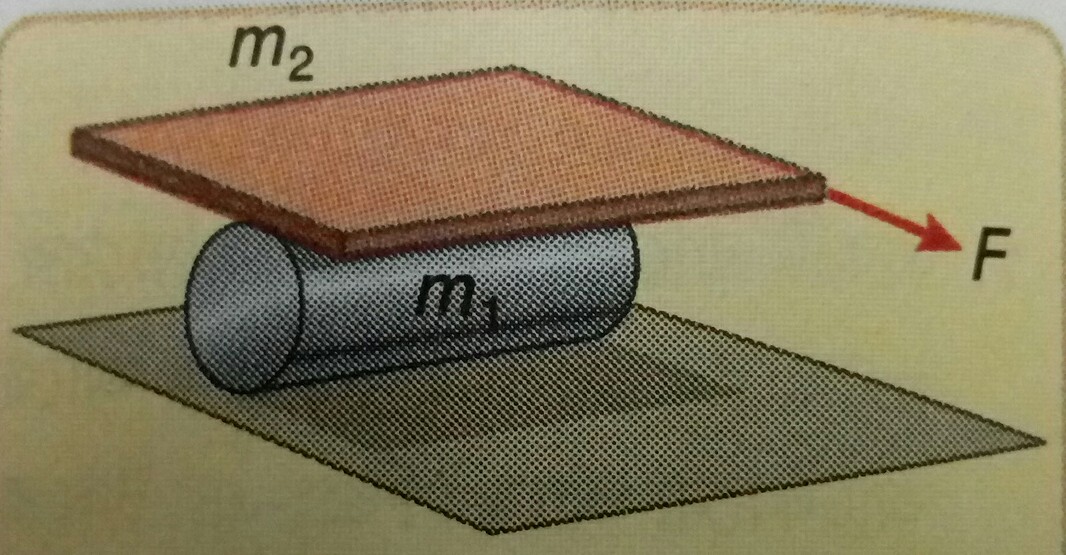
A man is pushing a cylinder of mass
i)acceleration of plank and center of mass of cylinder...
ii)Value of frictional force in the touching point and its direction.
1 Answer
Jan 29, 2018
See below.
Explanation:
The plank
The cylinder
but
i)
ii)
Here

