Optimization?
A light source is located over the center of a circular table of diameter 4 feet. (See picture below) Find the height h of the light source such that the illumination I at the perimeter of the table is maximum when
#l = \frac{ksin \alpha }{ s^{2}} #
where s is the slant, # \alpha# is the angle at which the light strikes the table and k is a constant.
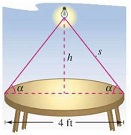
A light source is located over the center of a circular table of diameter 4 feet. (See picture below) Find the height h of the light source such that the illumination I at the perimeter of the table is maximum when
where s is the slant,

1 Answer
Write
Explanation:
We are given that
Use the definition of
So
That is:
Now use the Pythagorean Theorem to get
Now maximize as usual. (Find and test the critical points for
I get

