Question

P(a, b) is a point in the first quadrant. Circles are drawn through P touching the coordinate axes, such that the length of common chord of these circles is maximum, find the ratio a : b?

while solving the question, i realized that there will always be two such circles that can be drawn through P and satisfying the above criterion, with radius:
r1 = a+b+(2ab)^0.5 and r2 = a+b-(2ab)^0.5
the length of the common chord then turned out to be something like
L = root2*modulus(a-b)
if the question were to minimize this length, a : b would have easily been 1. but for maximising, woudn't the answer be infinity?

Answer 1

`a:b=3+-2sqrt2`

Explanation:

In order for a circle to be touching both coordinate axes in the first quadrant, it must have its center located on the line `y=x`, as seen below:

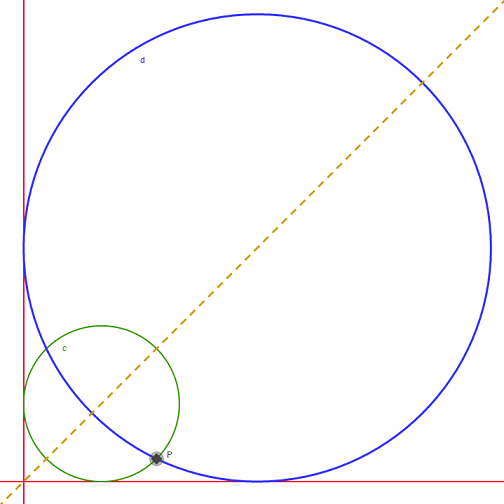
The common chord is going to be `PQ`, where `Q` is the symmetric point (a.k.a. the reflection) of `P` with respect to the line `y=x`, hence `Q` has coordinates `(b,a)`.

In order for the common chord to be the maximised, it has to be the diameter of the circle where `P` and `Q` are on its "high ends":

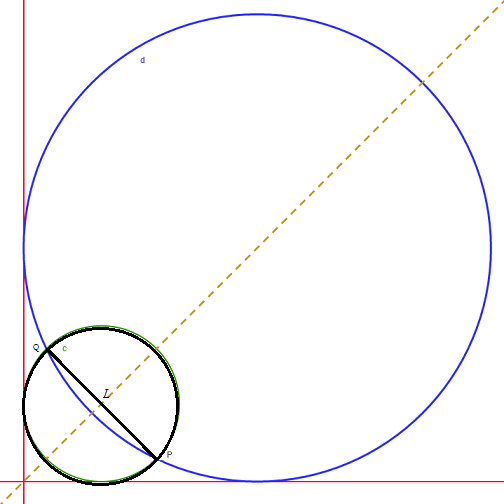
In our particular example, it almost overlaid one of the original circles.

Anyway, the center of this new circle is the midpoint of `PQ`, which we will denote `L`.

`L((a+b)/2,(a+b)/2)`

The equation of the circle is:

`(x-(a+b)/2)^2+(y-(a+b)/2)^2 = ((PQ)/2)^2`

The lenght of `PQ` is, as calculated by you, `sqrt2|a-b|`.

After some arithmetic, we reach the equation

`(x−a)(x−b)+(y−a)(y−b)=0`

The circle with diameter `PQ` must touch the axes as well, hence the points `((a+b)"/"2,0)` and `(0,(a+b)"/"2)` must be on it as well.

If we substitute the coordinates of one of these points (doesn't matter which; it gives us the same answer) into the circle equation we get the condition

`(a+b)^2=8ab`

`a^2+2ab+b^2=8ab`

`a^2-6ab+b^2=0`

Divide both sides by `b^2`:

`a^2/b^2 - 6a/b + 1 =0`

`(a/b)^2 - 6(a/b) + 1 =0`

This is a quadratic equation with the indeterminate the ratio of `a` and `b`, exactly what we want!

The solutions of this equation are

`a:b = 3+-2sqrt2`

These are the ratios we desire.